How does GEKKO optimization with bounded variables work?

Question

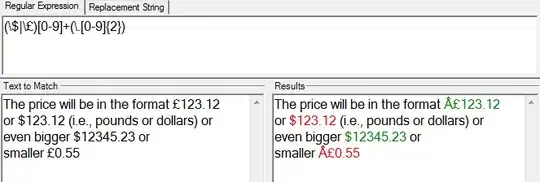
I am using GEKKO to estimate the parameters of a differential equation and I have bounded one of the variables between 0 and 1. However, when I solve the ODE, I get values outside of the bounds for this variable, so I was wondering if somebody knew how GEKKO finds the solution, as this might help me resolve the issue. Here is the code I use to fit the data. This gives me a solution x and u where x is between 0 and 1.

However, afterwards, I try to solve the ODE using scipy.integrate.solve_ivp, with the initial value of u that I got, and the solution I get for u is not between this bounds. Since it should be unique, I am wondering what is the process that GEKKO follows to find the solution (does it proyect the values to the bound or how does it deal with this?) Any comment is very appreciated.

Here is an MVCE. If you run it you can see that with GEKKO, I get a solution between the bounds and then, when I solve the ODE with solve_ivp, I don't get the same solution. Can you explain why this happens and how can I deal with it? I want to use solve_ivp to predict the next values.

from scipy.integrate import solve_ivp
from gekko import GEKKO
import matplotlib.pyplot as plt
time=[0.0, 0.11784511784511785, 0.18855218855218855,\
      0.2356902356902357]
m = GEKKO(remote=False)
m.time= [0.0, 0.11784511784511785, 0.18855218855218855,\
         0.2356902356902357]
x_data= [0.0003777630481280617, 0.002024573836061331,\
         0.0008954383363035536, 0.005331749410182463]
x = m.CV(value=x_data, lb=0); x.FSTATUS = 1 # fit to measurement
x.SPLO = 0
sigma = m.FV(value=0.5, lb= 0, ub=1); sigma.STATUS=1
d = m.Param(0.05)
k = m.Param(0.001)
b = m.Param(0.5)
r = m.FV(value=0.5, lb= 0); r.STATUS=1
m_param = m.Param(1)
u = m.Var(value=0.1, lb=0, ub=1)    
m.free(u)
a = m.Param(0.999)
Kmax= m.Param(100000)

m.Equations([x.dt()==x*(r*(1-a*u**2)*(1-x/(Kmax*(1-a*u**2)))-\
                        m_param/(k+b*u)-d), u.dt() == \
             sigma*((-2*a*(b**2)*r*(u**3)+4*a*b*k*r*(u**2)\
                     +2*a*(k**2)*r*u-b*m_param)/((b*u+k)**2))])
    
m.options.IMODE = 5  # dynamic estimation
m.options.NODES = 5   # collocation nodes
m.options.EV_TYPE = 1 # linear error (2 for squared)
m.solve(disp=False, debug=False)    # display solver output

def model_case_3(t, z, r, k, b, Kmax, sigma):
    m=1
    a=0.999
    x, u= z  
    dxdt =  x*(r*(1-a*u**2)*(1-x/(Kmax*(1-a*u**2)))-m/(k+b*u)-0.05)
    dudt = sigma*((-2*a*(b**2)*r*(u**3)+4*a*b*k*r*(u**2)\
                   +2*a*(k**2)*r*u-b*m)/((b*u+k)**2))
    return [dxdt, dudt]

sol = solve_ivp(fun=model_case_3, t_span=[0.0,  0.2356902356902357],\
                y0=[0.0003777630481280617, u.value[0]],\
                t_eval=[0.0, 0.11784511784511785, 0.18855218855218855,\
                        0.2356902356902357],  \
                args=(r.value[0], 0.001, 0.5,1000000 , sigma.value[0]))

fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(10,3), constrained_layout=True)
ax1.set_title('x')
ax1.plot(time, x.value, time, sol['y'][0])
ax2.set_title('u')
ax2.plot(time, u.value, time, sol['y'][1])
plt.show()

It is not an issue with the version of Gekko as I have Gekko 0.2.8, so I am wondering if it has anything to do with the initialization of variables. I run the example I posted on spyder (I was using google colab) and I got the correct solution, but when I run the rest of the cases I got again negative values for u (solving with solve_ivp), which is quite strange.

Could you post your code where the bound is not enforced? It may be that the solver is reporting an unsuccessful solution and the results can't be trusted. — John Hedengren, Nov 03 '20 at 18:07
You can check the solution status with `m.options.APPSTATUS` as shown https://apmonitor.com/wiki/index.php/Main/OptionApmAppstatus — Eric Hedengren, Nov 03 '20 at 18:18
What version of Gekko are you using? You may need to upgrade with `pip install gekko --upgrade`. — John Hedengren, Nov 04 '20 at 00:18

John Hedengren · Answer 1 · 2020-11-04T00:24:23.840

You can add a bound to a variable when it is created by setting lb (lower bound) and ub (upper bound).

z = m.Var(lb=0,ub=10)

After you create the variable, the bound is adjusted with .lower and .upper.

z.LOWER = 1
z.UPPER = 9

Here is an example problem that shows the use of bounds where x is constrained to be greater than 0.5.

from gekko import GEKKO

t_data = [0, 0.1, 0.2, 0.4, 0.8, 1]
x_data = [2.0,  1.6,  1.2, 0.7,  0.3,  0.15]

m = GEKKO(remote=False)
m.time = t_data
x = m.CV(value=x_data,lb=0.5,ub=3); x.FSTATUS = 1  # fit to measurement
k = m.FV(); k.STATUS = 1               # adjustable parameter
m.Equation(x.dt()== -k * x)            # differential equation

m.options.IMODE = 5   # dynamic estimation
m.options.NODES = 5   # collocation nodes
m.solve(disp=False)   # display solver output
k = k.value[0]; print(k)

A plot of the results shows that the bounds are enforced but the model prediction does not fit the data because of the lower bound constraint (x>=0.5).

import numpy as np
import matplotlib.pyplot as plt  # plot solution
plt.plot(m.time,x.value,'bo',\
         label='Predicted (k='+str(np.round(k,2))+')')
plt.plot(m.time,x_data,'rx',label='Measured')
# plot exact solution
t = np.linspace(0,1); xe = 2*np.exp(-k*t)
plt.plot(t,xe,'k:',label='Exact Solution')
plt.legend()
plt.xlabel('Time'), plt.ylabel('Value')
plt.show()

Without the restrictive lower bound, the solver optimizes to best fit the points.

x = m.CV(value=x_data,lb=0.0,ub=3)

Response 1 to Question Edit

The only way that a variable (such as u) is outside of the bounds is if the solver did not report a successful solution. To report a successful solution, the solver must satisfy the Karush Kuhn Tucker conditions for optimality. I recommend that you check that it satisfied all of the equations by checking that m.options.APPSTATUS==1 after the m.solve() command. If you can include an MVCE (https://stackoverflow.com/help/minimal-reproducible-example) that has sample data so the script can run, we can help you check it.

Response 2 to Question Edit

Thanks for including a minimal reproducible example. Here are the results that I get with Gekko 0.2.8. If you are using an earlier version, I recommend that you upgrade with pip install gekko --upgrade.

The solver reports a successful solution.

EXIT: Optimal Solution Found.

 The solution was found.

 The final value of the objective function is  0.03164650667928192
 
 ---------------------------------------------------
 Solver         :  IPOPT (v3.12)
 Solution time  :  0.23339999999999997 sec
 Objective      :  0.0316473666078486
 Successful solution
 ---------------------------------------------------

The constraints x>=0 and 0<=u<=1 are satisfied. Could it just be an issue with an older version of Gekko?

Thannks for your answer, but it does't really solve my problem, I edited the post to make my issue more clear. Also, you said that setting the bounds z = m.Var(lb=0,ub=10) is just for initialization, but when I used it, it bounds the u for every time point, not just the initial one. Did I misunderstand what you meant? — user606273, Nov 03 '20 at 21:14
I clarified the response: "initialization" is now "variable when it is created". I also edited the response with more information on how the solvers work. Here is the Interior Point method: https://apmonitor.com/me575/index.php/Main/InteriorPointMethod that is the method used by the default solver `IPOPT`. — John Hedengren, Nov 03 '20 at 22:26
If you need a bound that changes over time (such as changing from 0 to 0.5) then you could define `lower=m.Param([0,0,0.5,0.5,0.5])` and then add a new equation `m.Equation(x>lower)`. — John Hedengren, Nov 03 '20 at 22:34
Thanks, I added an MCVE as you suggested. The solver repports a successful solution, my problem is afterwards, when I try to solve the ODE (if I pass the same values for the parameters and initial conditions, shouldn't it be the same?) — user606273, Nov 03 '20 at 23:40
I added a response to your second edit. Is it just an outdated version of Gekko? — John Hedengren, Nov 04 '20 at 00:25
I just checked and it is not that, I have gekko 0.2.8. Can there be any settings that are different in my code and in yours? Like initial values of parameters or something? I just run it on Spyder and I got the same answer as you, however, on google colab I get the wrong answer. Could there be an issue with gekko and google colab?? — user606273, Nov 04 '20 at 08:55
Let us [continue this discussion in chat](https://chat.stackoverflow.com/rooms/224109/discussion-between-user606273-and-john-hedengren). — user606273, Nov 04 '20 at 18:04

How does GEKKO optimization with bounded variables work?

1 Answers1