My question involves a bounded root finding problem for when the function behaves strangely when it is near zero.
Setup
I am trying to find the root for the following equation
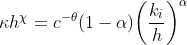
where

kappa, chi, theta and alpha are all parameters that I set. the variable k is a 30 by 30 grid.
I am trying to find the root for h evaluating at all k grid points. The root should return an h that is between the bounds 0 and 1. The function is increasing, but in areas when h is close to zero (usually less than 0.1) it will cross the x-axis twice. This occurs for some grid points that I evaluate at and others it does not happen. In theory this shouldn't happen. So when I evaluate at grid points using bisection methods like bisect and brentq at most grid points it works but for some I will get an error "f(a) and f(b) positive".
So I instead trying to turn the root finding problem in a minimization problem where I square the function and use brent function. But I am still running into similar problems like before. However this time it will stop because of too many iterations and many of the solutions are not in the specified bounds.
for i in range(nk):
for j in range(nk):
def foch(n):
return (kappa*n**chi - (kgrid[i]**(alpha)*n**(1-alpha) +
(1-delta)*kgrid[i] -
kgrid[j])**(-theta)*(1-alpha)*(kgrid[i])**(alpha)*n**(-alpha))**2
res[i,j] =opt.brent(foch, brack=(10e-3, 1))
Question
How can I find the root to this equation which in theory is unique? Is there an alternative method that I could use than standard root-finding or minimazation problems?
Code
import numpy as np
import scipy.optimize as opt
##### parameters #####
beta, alpha, delta, theta, chi = 0.988, 0.321, 0.013, 1, 0.5
#number of grid points.
nk = 30
#setting up the grid
kstar = (1/3)*(alpha/(1/beta - (1-delta)))**(1/(1 - alpha))
kmin=0.25*kstar
kmax=1.75*kstar
kgrid = np.linspace(kmin, kmax, nk)
#set ss labor hours
nstar=.2925
cstar = kstar**alpha*nstar**(1-alpha) - delta*kstar
#endogenously determine kappa
kappa=(1/nstar**chi)*cstar**(-theta)*(1-alpha)*(kstar/nstar)**alpha
#### solve ####
res=np.empty((nk, nk))
for i in range(nk):
for j in range(nk):
def foch(n):
return (kappa*n**chi - (kgrid[i]**(alpha)*n**(1-alpha) +
(1-delta)*kgrid[i] -
kgrid[j])**(-theta)*(1-alpha)*(kgrid[i])**(alpha)*n**(-alpha))**2
res[i,j] =opt.brent(foch, brack=(10e-3, 1))