For starters we can handle your data as point cloud (polygon vertexes) p[i] and some circle defined by center p0 and radius r. If your point cloud is entirely inside circle you can ignore the radius.
We can exploit atan2 however to avoid problems with crossing and sector selection we do not enlarge min/max bounds as usual for standard cartesian BBOX computation instead:
compute atan2 angle for each point and remember it in array a[]
sort a[]
find biggest distance between consequent angles in a[]
Do not forget that angle difference can be |Pi| tops so if it is more you need to +/- 2*PI. Also handle a[] as cyclic buffer.
This is my simple C++/VCL attempt:
//---------------------------------------------------------------------------
float p0[]={52.87404,30.856130,42.55699,28.46292,41.54373,24.319989,53.57623,21.300564,62.94891,28.46292,49.39652,27.550071,52.87404,30.85613,};
float p1[]={52.94294,30.920592,42.55699,28.46292,43.61965,35.545578,55.85037,34.862696,59.12524,36.621547,47.68664,39.877048,35.69973,36.198265,37.30512,29.196711,31.09762,28.46292,41.54373,24.319989,53.57623,21.300564,62.94891,28.46292,49.39652,27.550071,52.94294,30.920592,};
float p2[]={52.94294,30.920592,42.55699,28.46292,43.61965,35.545578,52.45594,37.266299,59.30560,29.196711,64.12177,33.290489,58.81733,36.554277,47.68664,39.877048,35.69973,36.198265,37.30512,29.196711,31.09762,28.46292,41.54373,24.319989,53.57623,21.300564,62.94891,28.46292,49.39652,27.550071,52.94294,30.920592,};
float x0=45.0,y0=30.0,R=25.0;
//---------------------------------------------------------------------------
template <class T> void sort_asc_bubble(T *a,int n)
{
int i,e; T a0,a1;
for (e=1;e;n--) // loop until no swap occurs
for (e=0,a0=a[0],a1=a[1],i=1;i<n;a0=a1,i++,a1=a[i])// proces unsorted part of array
if (a0>a1) // condition if swap needed
{ a[i-1]=a1; a[i]=a0; a1=a0; e=1; } // swap and allow to process array again
}
//---------------------------------------------------------------------------
void get_sector(float x0,float y0,float r,float *p,int n,float &a0,float &a1)
{
// x0,y0 circle center
// r circle radius
// p[n] polyline vertexes
// a0,a1 output angle range a0<=a1
int i,j,m=n>>1;
float x,y,*a;
a=new float[m];
// process points and compute angles
for (j=0,i=0;i<n;j++)
{
x=p[i]-x0; i++;
y=p[i]-y0; i++;
a[j]=atan2(y,x);
}
// sort by angle
sort_asc_bubble(a,m);
// get max distance
a0=a[m-1]; a1=a[0]; x=a1-a0;
while (x<-M_PI) x+=2.0*M_PI;
while (x>+M_PI) x-=2.0*M_PI;
if (x<0.0) x=-x;
for (j=1;j<m;j++)
{
y=a[j]-a[j-1];
while (y<-M_PI) y+=2.0*M_PI;
while (y>+M_PI) y-=2.0*M_PI;
if (y<0.0) y=-y;
if (y>x){ a0=a[j-1]; a1=a[j]; x=y; }
}
}
//---------------------------------------------------------------------------
void TMain::draw()
{
int i,n;
float x,y,r,*p,a0=0.0,a1=0.0;
float ax,ay,bx,by;
float zoom=7.0;
p=p0; n=sizeof(p0)/sizeof(p0[0]);
// p=p1; n=sizeof(p1)/sizeof(p1[0]);
// p=p2; n=sizeof(p2)/sizeof(p2[0]);
get_sector(x0,y0,R,p,n,a0,a1);
// clear buffer
bmp->Canvas->Brush->Color=clBlack;
bmp->Canvas->FillRect(TRect(0,0,xs,ys));
// circle
x=x0; y=y0; r=R;
ax=x+R*cos(a0);
ay=y+R*sin(a0);
bx=x+R*cos(a1);
by=y+R*sin(a1);
x*=zoom; y*=zoom; r*=zoom;
ax*=zoom; ay*=zoom;
bx*=zoom; by*=zoom;
bmp->Canvas->Pen->Color=clBlue;
bmp->Canvas->Brush->Color=TColor(0x00101010);
bmp->Canvas->Ellipse(x-r,y-r,x+r,y+r);
bmp->Canvas->Pen->Color=clAqua;
bmp->Canvas->Brush->Color=TColor(0x00202020);
bmp->Canvas->Pie(x-r,y-r,x+r,y+r,ax,ay,bx,by);
// PCL
r=2.0;
bmp->Canvas->Pen->Color=clAqua;
bmp->Canvas->Brush->Color=clAqua;
for (i=0;i<n;)
{
x=p[i]; i++;
y=p[i]; i++;
x*=zoom; y*=zoom;
bmp->Canvas->Ellipse(x-r,y-r,x+r,y+r);
}
// render backbuffer
Main->Canvas->Draw(0,0,bmp);
}
//---------------------------------------------------------------------------
You can ignore the void TMain::draw() function its just example of usage and this is the preview:
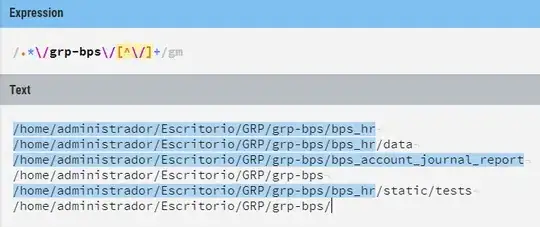
However as you have polygon (lines) to avoid wrong results You have two simple options:
sample lines with more than just 2 points
this way the angular gap should be bigger than distances between points in the point cloud. So if you sample lines with enough points the result will be correct. However wrongly selected number of points per line will lead to wrong result in edge cases. On the other hand implementing this is just simple DDA interpolation added to current code.
convert to handling angle intervals instead of angles a[]
so for each line compute angular interval <a0,a1> with predefined poygon winding rule (so CW or CCW but consistent). And instead of array a[] you would have ordered list of intervals where you would either insert new interval or merge with existing if overlap. This approach is safe but merging angular intervals is not that easy. If the input data is polyline (like yours) that means each next line start from the previous line endpoint so you can ignore the list of intervals and just enlarge the single one instead but still you need to handle the enlargement correctly which is not trivial.
[Edit1] using the first approach the updated function look like this:
void get_sector_pol(float x0,float y0,float r,float *p,int n,float &a0,float &a1)
{
// x0,y0 circle center
// r circle radius
// p[n] point cloud
// a0,a1 output angle range a0<=a1
int i,j,k,N=10,m=(n>>1)*N;
float ax,ay,bx,by,x,y,dx,dy,*a,_N=1.0/N;
a=new float[m];
// process points and compute angles
bx=p[n-2]-x0; i++;
by=p[n-1]-y0; i++;
for (j=0,i=0;i<n;)
{
ax=bx; ay=by;
bx=p[i]-x0; i++;
by=p[i]-y0; i++;
dx=_N*(bx-ax); x=ax;
dy=_N*(by-ay); y=ay;
for (k=0;k<N;k++,x+=dx,y+=dy,j++) a[j]=atan2(y,x);
}
// sort by angle
sort_asc_bubble(a,m);
// get max distance
a0=a[m-1]; a1=a[0]; x=a1-a0;
while (x<-M_PI) x+=2.0*M_PI;
while (x>+M_PI) x-=2.0*M_PI;
if (x<0.0) x=-x;
for (j=1;j<m;j++)
{
y=a[j]-a[j-1];
while (y<-M_PI) y+=2.0*M_PI;
while (y>+M_PI) y-=2.0*M_PI;
if (y<0.0) y=-y;
if (y>x){ a0=a[j-1]; a1=a[j]; x=y; }
}
}
As you can see its almost the same just simple DDA is added to the first loop win N points per line. Here preview for the second polygon which fails with just point cloud approach: