Note: Another method to attempt may include moving/windowing averages to calculate the local amount to offset by.
Method 1: Discrete Cosine Transform (DC Offset Removal)
Converts the image into the frequency domain uses the Discrete Fourier Transform (DCT). Removes the DC coefficient in the top-left corner (set to zero) of the matrix and convert it back to the spatial domain using the Inverse Discrete Fourier Transform (IDCT).
Image = imread("Test_Image.jpg");
%Converting image to greyscale if RGB image%
[Image_Height,Image_Width,Depth] = size(Image);
if(Depth == 3)
Image = rgb2gray(Image);
end
%Removing image offset%
Discrete_Cosine_Transformed_Image = dct2(Image);
Discrete_Cosine_Transformed_Image(1,1) = 0;
Inverse_Discrete_Cosine_Transformed_Image = idct2(Discrete_Cosine_Transformed_Image);
Calibrated_Image = medfilt2(Inverse_Discrete_Cosine_Transformed_Image,[20 20]);
% Plotting the original and thresholded image%
X_Axes = (1:1:Image_Height);
Y_Axes = (1:1:Image_Width);
subplot(1,2,1); surf(X_Axes,Y_Axes,Image,'EdgeColor','none');
title("Original Image Plot");
xlabel('X-Axis'); ylabel('Y-Label');
zlim([0 255]);
subplot(1,2,2); surf(X_Axes,Y_Axes,uint8(Calibrated_Image),'EdgeColor','none');
title("Calibrated Image Plot");
xlabel('X-Axis'); ylabel('Y-Label');
zlim([0 255]);
Key Discrete Cosine Transform (DCT) Filtering Code Lines
%Removing image offset%
Discrete_Cosine_Transformed_Image = dct2(Image);
Discrete_Cosine_Transformed_Image(1,1) = 0;
Inverse_Discrete_Cosine_Transformed_Image = idct2(Discrete_Cosine_Transformed_Image)
Method 2: Standard Uniform Offset (no-tilt accommodation)
Uses a constant value and subtracts that across the whole image matrix.
Test Image 1: Using Lowest Intensity to Calculate Offset
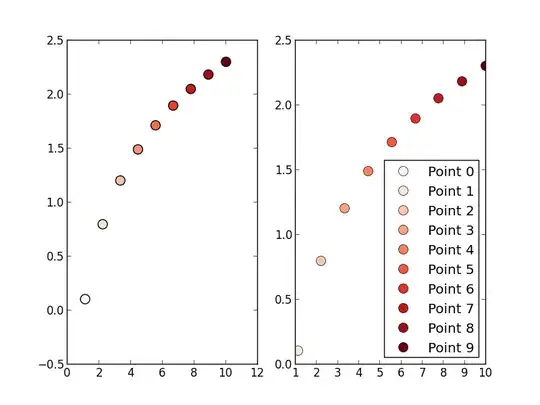
Test Image 2: Using Average/Mean to Calculate Offset
Image = imread("Circular_Image.png");
%Converting image to greyscale if RGB image%
[Image_Height,Image_Width,Depth] = size(Image);
if(Depth == 3)
Image = rgb2gray(Image);
end
%Removing image offset%
Lowest_Intensity_Value = min(Image,[],'all');
Average = mean(Image,'all');
Calibrated_Image = Image - Average;
% Plotting the original and thresholded image%
X_Axes = (1:1:Image_Height);
Y_Axes = (1:1:Image_Width);
subplot(1,2,1); surf(X_Axes,Y_Axes,Image,'EdgeColor','none');
title("Original Image Plot");
xlabel('X-Axis'); ylabel('Y-Label');
zlim([0 255]);
subplot(1,2,2); surf(X_Axes,Y_Axes,Calibrated_Image,'EdgeColor','none');
title("Calibrated Image Plot");
xlabel('X-Axis'); ylabel('Y-Label');
zlim([0 255]);
Using MATLAB version: R2019b