1

Background: I observe a sample of a variable z that is the sum of two independent and identically distributed variables x and y. I'm trying to recover the distribution of x, y (call it f) from the distribution of z (call it g), under the assumption that f is symmetric about zero. According to Horowitz and Markatou (1996) we have that the Fourier Transform of f is equal to sqrt(|G|), where G is the Fourier transform of g.

Example:

import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import gaussian_kde, laplace


# sample size
size = 10000
# Number of points to preform FFT on
N = 501
# Scale of the laplace rvs
scale = 3.0

# Test deconvolution
laplace_f = laplace(scale=scale)
x = laplace_f.rvs(size=size)
y = laplace_f.rvs(size=size)
z = x + y
t = np.linspace(-4 * scale, 4 * scale, size)
laplace_pdf = laplace_f.pdf(t)
t2 = np.linspace(-4 * scale, 4 * scale, N)

# Get density from z. Kind of cheating using gaussian
z_density = gaussian_kde(z)(t2)
z_density = (z_density + z_density[::-1]) / 2
z_density_half = z_density[:((N - 1) // 2) + 1]
ft_z_density = np.fft.hfft(z_density_half)
inv_fz_density = np.fft.ihfft(np.sqrt(np.abs(ft_z_density)))
inv_fz_density = np.r_[inv_fz_density, inv_fz_density[::-1][:-1]]
f_deconv_shifted = np.real(np.fft.fftshift(inv_fz_density))
f_deconv = np.real(inv_fz_density)

# Normalize to be a pdf
f_deconv_shifted /= f_deconv_shifted.mean()
f_deconv /= f_deconv.mean()

# Plot
plt.subplot(221)
plt.plot(t, laplace_pdf)
plt.title('laplace pdf')

plt.subplot(222)
plt.plot(t2, z_density)
plt.title("z density")

plt.subplot(223)
plt.plot(t2, f_deconv_shifted)
plt.title('Deconvolved with shift')

plt.subplot(224)
plt.plot(t2, f_deconv)
plt.title('Deconvolved without shift')

plt.tight_layout()
plt.show()

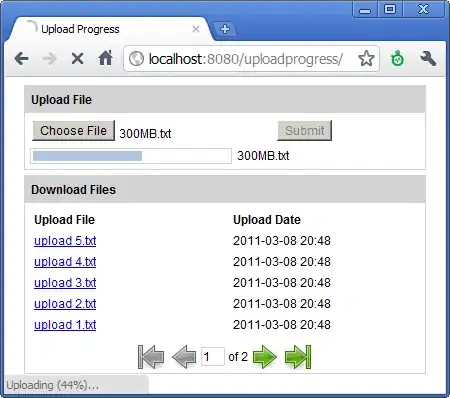
Which results in enter image description here

Issue: there's clearly something wrong here. I don't think I should need the shift, yet the shifted pdf seems to be closer to the truth. I suspect it has something to do with the domain of the IFFT changing with the sqrt(abs()) operation, but I'm really not sure.

BVJ
  • 568
  • 4
  • 18
  • This is because the FFT assumes that the origin is the first element of the data array, whereas you place the origin in the middle of this array. The shift in the spatial domain is a phase term in the frequency domain, but you eliminate the phase (use the magnitude only), hence you “unshift” the signal in the spatial domain, making it symmetric around the origin. – Cris Luengo Oct 05 '20 at 23:15
  • Thanks @CrisLuengo! I didn't realize that and it makes sense. If you want to add it as an answer I'll accept it and close this. – BVJ Oct 06 '20 at 03:55

1 Answers1

0

The FFT is defined such that the times associated to the input samples are t=0..N-1. That is, the origin is in the first sample. The same is true for the output, the associated frequencies are k=0..N-1.

Your distribution is symmetric about zero, but ignoring your t (which you cannot pass to the FFT function), and knowing what the t values are that are implied by the FFT definition, you can see that your distribution is actually shifted, which adds a phase component to the frequency domain. You ignore the phase there (by using hfft instead of fft, which means you shift your input signal such that it becomes symmetric about the origin as defined by the FFT (not your origin).

fftshift shifts the signal resulting from the IFFT such that the origin is back where you want it to be. I recommend that you use ifftshift before calling hfft, just to ensure that your signal is actually symmetric as expected by that function. I don't know if it will make a difference, it depends on how this function is implemented.

Cris Luengo
  • 55,762
  • 10
  • 62
  • 120