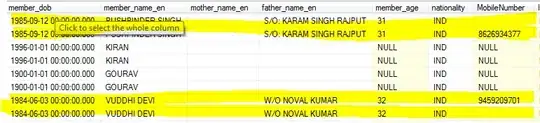
So my idea is (borrowed from neural network folks) that if I have data set D, I can fit a quadratic curve to it by first calculating the derivative of the error with respect to the parameters (a, b, and c), and then do a small update that minimizes the error. My problem is, the following code doesn't actually manage fit the curve. For linear stuff, a similar approach works, but quadratic seems to fail for some reason. Can you see what I have done wrong (either assumption or just implementation error)
EDIT: The question was not specific enough: This following code will not deal with bias in data very well. For some reason it updates a and b parameters somehow that c gets left behind. This method is similar to robotics (find path using Jacobians) and neural networks (find parameters based on error) so it is not unreasonable algorithm, now the question is, why this specific implementation does not produce results that I would expect.
In the following Python code, I use math as m, and MSE is a function that calculates Mean Squared Error between two arrays. Other than that, the code is self contained
Code:
def quadraticRegression(data, dErr):
a = 1 #Starting values
b = 1
c = 1
a_momentum = 0 #Momentum to counter steady state error
b_momentum = 0
c_momentum = 0
estimate = [a*x**2 + b*x + c for x in range(len(data))] #Estimate curve
error = MSE(data, estimate) #Get errors 'n stuff
errorOld = 0
lr = 0.0000000001 #learning rate
while abs(error - errorOld) > dErr:
#Fit a (dE/da)
deda = sum([ 2*x**2 * (a*x**2 + b*x + c - data[x]) for x in range(len(data)) ])/len(data)
correction = deda*lr
a_momentum = (a_momentum)*0.99 + correction*0.1 #0.99 is to slow down momentum when correction speed changes
a = a - correction - a_momentum
#fit b (dE/db)
dedb = sum([ 2*x*(a*x**2 + b*x + c - data[x]) for x in range(len(data))])/len(data)
correction = dedb*lr
b_momentum = (b_momentum)*0.99 + correction*0.1
b = b - correction - b_momentum
#fit c (dE/dc)
dedc = sum([ 2*(a*x**2 + b*x + c - data[x]) for x in range(len(data))])/len(data)
correction = dedc*lr
c_momentum = (c_momentum)*0.99 + correction*0.1
c = c - correction - c_momentum
#Update model and find errors
estimate = [a*x**2 +b*x + c for x in range(len(data))]
errorOld = error
print(error)
error = MSE(data, estimate)
return a, b, c, error