0

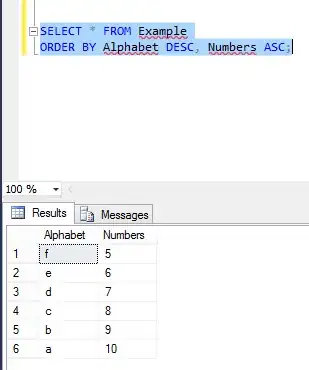
I have two points A(x1,y1) & B(x2,y2) of a line, I need to check if the third point say C(x3,y3) falls anywhere within 1 meters range on both sides of the line. So, when AB forms a horizontal line we check in the area 1 meter above and 1 meter below the line. And if the line is vertical then third point should be on left side or right side of the line in the range of 0 to 10meters from AB. (point C could be on line AB or in the range of 10 meters)

I could use slope intercept or point intercept if I just wanted to check on the line but I need to give a buffer of 1 meter around the line formed.Please help.Thanks.

point c shown through black text are within the area & red ones are out of the allowed area. enter image description here

Reblochon Masque
  • 35,405
  • 10
  • 55
  • 80
rani
  • 9
  • 2
  • I don't think `java` is a valid tag for this question and also I believe a better forum for this should be Math Exchange and not stack overflow is it more of a mathematical question. – adnaan.zohran Sep 24 '20 at 19:42
  • you are correct, but its sort of a desperate attempt to get to a solution given my math is so bad.I've uploaded the same question on math forum as well! – rani Sep 24 '20 at 20:05
  • You could convert my [C# code here](https://stackoverflow.com/a/42332379/2330053)... – Idle_Mind Sep 24 '20 at 23:21
  • thanks so much! I'm not sure I got the role of q correct.// q is the parameterized value needed to get to the intersection q = ((Px - Ax) * (Bx - Ax) + (Py - Ay) * (By - Ay)) / ((Bx - Ax) * (Bx - Ax) + (By - Ay) * (By - Ay)); // Limit q to 0 <= q <= 1 // If q is outside this range then the Point is somewhere past the // endpoints of our segment. By setting q = 0 or q = 1 we are // measuring the actual distacne from the point to one of the // endpoints(instead) – rani Sep 25 '20 at 03:36
  • I can use your solution, just need help with why you've kept the value of q to either 0 or 1 . – rani Sep 25 '20 at 03:46
  • The [explanation at the top here](http://vb-helper.com/howto_distance_point_to_line.html) is good. – Idle_Mind Sep 25 '20 at 04:35
  • thank you so much! the explanation there is very helpful. this solves my problem:) – rani Sep 26 '20 at 19:29

2 Answers2

0

The smallest distance between the line formed by the points (X1, Y1) and (X2, Y2), and the point (X3, Y3) is:

distance = abs((Y3 - Y1) * (X2 - X1) - (Y2 - Y1) * (X3 - X1))

You can check if that distance is smaller than 1 meter.

MrPontes
  • 29
  • 5
  • thanks, what about the direction/slope of point C. It could be at any angle with respect to A & B. Does this equation take care of that as well ? – rani Sep 24 '20 at 20:02
  • If you remove the abs, the result could be either positive or negative, depending on which side of the line the point is. The equation only gives you the smallest distance (with a 90 degree angle). We don't know anything about the angle. – MrPontes Sep 24 '20 at 20:20
  • okay, could you please tell me what this equation is called so that I could go through all the cases once and understand it before I code it. – rani Sep 25 '20 at 03:29
  • This is not the right formula. (It yields an area, not a distance.) –  Sep 25 '20 at 07:52
  • The exact test can be written `((Y3 - Y1) * (X2 - X1) - (Y2 - Y1) * (X3 - X1))² ≤ D² ((X2 - X1)² + (Y2 - Y1)²)`. –  Sep 25 '20 at 07:55
0

MrPontes is close to the truth but forgot a normalization factor. I am giving another solution that uses complex numbers. Let the three points be given by the complex numbers Za, Zb and Zc.

The formula for the distance of C to the line AB is

D = Im((Zc - Za) / (Zb - Za)) |Zb - Za|

(Im denotes the imaginary part). This distance is positive on one side and negative on the other, you can take the absolute value.

Explanation:

If we subtract Za from the points, A goes to the origin and the others follow.

If we now divide by Zb - Za, B goes to the point 1 by a rotation around the origin and a scaling by 1/|Zb - Za|. We undo the scaling to get a pure rotation.

Now

(Zc - Za) / (Zb - Za) |Zb - Za|

applies to C the rotation that brings AB to the horizontal axis X, and the requested distance is the ordinate of the transformed C.

  • thanks so much for the answer but I have point coordinates available to me and Im getting the projection point & finding the distance between point C & its projection on the line AB(http://vb-helper.com/howto_distance_point_to_line.html). Could you please help me as to how I can get the complex numbers from point coordinates. Also,Im not clear on the value of the imaginary part. I want to check your solution too as this seems more efficient once I get the complex numbers. This might be a very basic question but my math is not that good.ur help would be appreciated.thanks. – rani Sep 26 '20 at 19:43
  • @rani: this solution is more compact in terms of formulas, but when you evaluate it, you get the same result as in MrPontes' answer (after fixing it). Use the expression in my comment to his post. –  Sep 27 '20 at 10:14