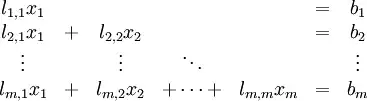Fast and efficient upper diagonal matrix inverse

Question

I compute the multinomial Gaussian density for some huge number of times in a project where I update the covariance matrix by rank-1. Instead of computing the covariance from scratch, I used the cholupdate function to add a new sample to the covariance and remove a new sample to the covariance. By this way, the update is told to be in $O(n^2)$ as opposed to $O(n^3)$ Cholesky factorization of the covariance matrix.

persistent R
if (initialize) % or isempty(R)
    % compute covariance V
    R = chol(V);
else
    R = cholupdate(R,xAdded);

detVar = prod(diag(R))^2;
Rt = R';
coeff = 1/sqrt((2*pi)^dimension*detVar);
y = Rt\x;
logp = log(coeff) - 1/2 * norm(y)^2;

Actually the code is quite complicated but I simplified it here. I wonder if there is a faster way to compute the inverse (the Rt\x part in the code) of an upper triangular matrix in MATLAB. Do you have any ideas to do it more efficiently in MATLAB.

Note that computing the determinant is also faster this way. So the new method will also not bad for the computation of the determinant.

Answer 1

The mldivide function is smart enough to check for triangular matrices, in which case it uses a forward/backward substitution method to efficiently solve the linear system:

AX=B  <-->  X=inv(A)*B  <-->  X=A\B

(compute x1, substitute it in second equation and compute x2, substitute in third ...)