Performance when Generating CPU Cache Misses

Question

I am trying to learn about CPU cache performance in the world of .NET. Specifically I am working through Igor Ostovsky's article about Processor Cache Effects.

I have gone through the first three examples in his article and have recorded results that widely differ from his. I think I must be doing something wrong because the performance on my machine is showing almost the exact opposite results of what he shows in his article. I am not seeing the large effects from cache misses that I would expect.

What am I doing wrong? (bad code, compiler setting, etc.)

Here are the performance results on my machine:

enter image description here

If it helps, the processor on my machine is an Intel Core i7-2630QM. Here is info on my processor's cache:

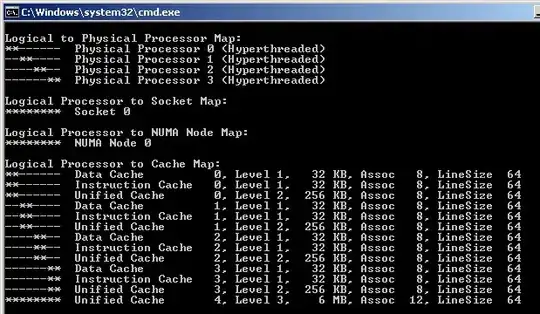
enter image description here

I have compiled in x64 Release mode.

Below is my source code:

class Program
    {

        static Stopwatch watch = new Stopwatch();

        static int[] arr = new int[64 * 1024 * 1024];

        static void Main(string[] args)
        {
            Example1();
            Example2();
            Example3();


            Console.ReadLine();
        }

        static void Example1()
        {
            Console.WriteLine("Example 1:");

            // Loop 1
            watch.Restart();
            for (int i = 0; i < arr.Length; i++) arr[i] *= 3;
            watch.Stop();
            Console.WriteLine("     Loop 1: " + watch.ElapsedMilliseconds.ToString() + " ms");

            // Loop 2
            watch.Restart();
            for (int i = 0; i < arr.Length; i += 32) arr[i] *= 3;
            watch.Stop();
            Console.WriteLine("     Loop 2: " + watch.ElapsedMilliseconds.ToString() + " ms");

            Console.WriteLine();
        }

        static void Example2()
        {

            Console.WriteLine("Example 2:");

            for (int k = 1; k <= 1024; k *= 2)
            {

                watch.Restart();
                for (int i = 0; i < arr.Length; i += k) arr[i] *= 3;
                watch.Stop();
                Console.WriteLine("     K = "+ k + ": " + watch.ElapsedMilliseconds.ToString() + " ms");

            }
            Console.WriteLine();
        }

        static void Example3()
        {   

            Console.WriteLine("Example 3:");

            for (int k = 1; k <= 1024*1024; k *= 2)
            {

                //256* 4bytes per 32 bit int * k = k Kilobytes
                arr = new int[256*k];



                int steps = 64 * 1024 * 1024; // Arbitrary number of steps
                int lengthMod = arr.Length - 1;

                watch.Restart();
                for (int i = 0; i < steps; i++)
                {
                    arr[(i * 16) & lengthMod]++; // (x & lengthMod) is equal to (x % arr.Length)
                }

                watch.Stop();
                Console.WriteLine("     Array size = " + arr.Length * 4 + " bytes: " + (int)(watch.Elapsed.TotalMilliseconds * 1000000.0 / arr.Length) + " nanoseconds per element");

            }
            Console.WriteLine();
        }

    }

What CPU are you using? How much cache does it have? Level1 and 2? — Oded, Jun 18 '11 at 13:13
It is a Intel Core i7-2630QM. The cache stats are in the command line image above. — Jason Moore, Jun 18 '11 at 13:19
Also, you have enough RAM in the system? You're not thrashing on the pagefile during the test? — Chris O, Jun 18 '11 at 13:19
8 GB of RAM on my machine. When running this console app, RAM usage never gets above 4GB. — Jason Moore, Jun 18 '11 at 13:23
You can safely assume the author did not nearly have as nice a core as you do. The inherent 1/K perf of the test loop emphasizes his results but obfuscates yours. — Hans Passant, Jun 18 '11 at 15:08

score 3 · Accepted Answer · answered Jun 22 '11 at 15:57

3

Why are you using i += 32 in the second loop. You are stepping over cache lines in this way. 32*4 = 128bytes way bigger then 64bytes needed.

answered Jun 22 '11 at 15:57

DiVan

381
2
6

2

...I don't understand this answer. Why does that account for the order-of-magnitude difference, and what does that have to do with the second or third tests? – BlueRaja - Danny Pflughoeft May 01 '13 at 18:33
1

Even knowing this is quite old, just for someone else reference, the cache lines are typically fetched in chunks of 64 bytes, so what DiVan is showing is that in an **int** (4 bytes) array, whether you traverse it stepping by 32 you'll end jumping over more than one cache line, what will of course make the loop 2 faster, if you were using 16 instead of 32 (16x4=64), then you won't skip any cache lines and loop 1 and 2 will have a similar result, even loop 2 iterating less times than loop 1. – DenninDalke Mar 19 '17 at 14:51

Performance when Generating CPU Cache Misses

1 Answers1