10

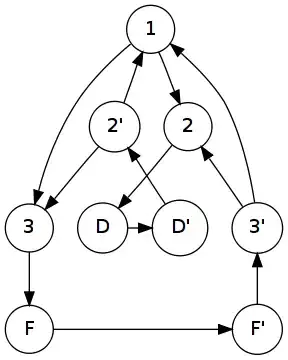
A simple way to represent a graph is with a data structure of the form:

{1:[2,3],
 2:[1,3],
 3:[1,2]}

Where the keys in this dictionary are nodes, and the edges are represented by a list of other nodes they are connected to. This data structure could also easily represent a directed graph if the links are not symmetrical:

{1:[2],
 2:[3],
 3:[1]}

I don't know much about the graph-theory, so what I'm about to propose might already have a simple solution, but I don't know what to look for. I've encountered what I think is a situation where a graph is somewhat directed, depending on both the node you're at, and the node you came from. To illustrate, I have a drawing:

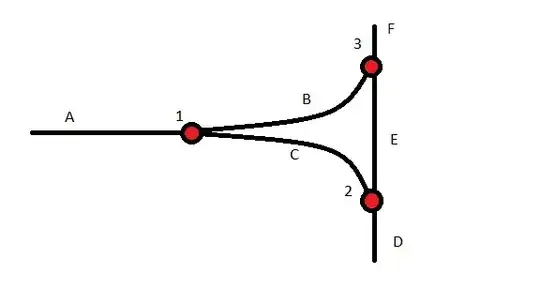
Strangely Directional Graph

Imagine you're speeding along edge A in a go-kart and at node 1 you hang a left onto edge B. Since you're going so fast, when you hit node 3, you're forced to continue onto edge F. However, if you were coming from edge F, you would be able to go on to either edge E or B. It is clear that node three is connected to 1 and 2, but whether or not you can reach them from that node depends on which direction you came from.

I'm wondering if there is a graph theory concept that describes this and/or if there is a simple data structure to describe it. While I'll be writing my code in python, I'll take advice coming from any reasonably applicable language.

Edit: I tried to post an image to go along with this, but I'm not sure if it's showing up. If it isn't here's a link to the image

Edit 2: I should have been clear. The image posted is meant to be a portion of a complete graph, in which there are more nodes off screen from A, D, and F.

Wilduck
  • 13,822
  • 10
  • 58
  • 90

3 Answers3

7

This could be represented by a directed graph.

Nodes in your graph could be represented as two nodes in the graph. Think of the nodes as representing locations on particular sides of a street -- the edges being like inbound and outbound lanes.

enter image description here

unutbu
  • 842,883
  • 184
  • 1,785
  • 1,677
  • I don't think that's what I'm looking for. Each node is only directed depending on where you came from. If it is what I'm looking for in this case, could you explain a little better how it applies? – Wilduck Jun 16 '11 at 18:18
  • The question states that it is not a directed graph. The direction of an edge is determined by which node you just passed. – mwcz Jun 16 '11 at 18:19
  • Ignore my comment. The answer was edited and is more fitting now. :) – mwcz Jun 16 '11 at 18:26
  • While I can imagine how this could look like a two way street, I guess I was looking for a slightly better answer. I wanted to leverage the fact that any properties of the edges (such as length, weight, etc) would be the same no matter what direction their being traveled. While this is probably possible to enforce with a DAG, I was hoping for something that showed this was necessarily the case... – Wilduck Jun 16 '11 at 20:24
  • Why does the graph have to be acyclic? I think a directed graph is appropriate, but not an acyclic one. In fact, the graph in the diagram has several cycles. – RoundTower Jun 16 '11 at 20:45
1

You could implement it as a basic graph with nodes and edges. In each node, store a list of edges. For each of those edges, store a mapping from that "entry" edge, to the valid exit edges.

I should point out that the image you posted isn't a graph, since A, F, and D do not connect to any nodes (unless they're just off-screen).

mwcz
  • 8,949
  • 10
  • 42
  • 63
  • 1
    I guess I should have been explicit, but yes, I was trying to imply that there was more nodes off screen. – Wilduck Jun 16 '11 at 18:32
1

Represent your graph as a mapping of strings to mapping of strings to sets.

To be more clear, in python you would have:

graph = {
    'A': {
        'B': set(['C', 'D', ...]),
        'E': set(['F']),
    },
    ...
}

An edge exists between A and B if the key B is contained by the entry A in the graph mapping.

This edge can be walked if the node from which we come from is contained in the set mapped to by graph['A']['B'].

The following python class implements this specification (you can find a commented version on this gist):

class Graph(object):
    def __init__(self):
        self.nodes = {}

    def addEdge(self, (node1, comingFrom1), (node2, comingFrom2)):
        self.nodes.setdefault(node1, {})[node2] = comingFrom1
        self.nodes.setdefault(node2, {})[node1] = comingFrom2

    def isEdge(self, comingFrom, passingBy, goingTo):
        try:
            return comingFrom in self.nodes[passingBy][goingTo]
        except KeyError:
            return False

    def destinations(self, comingFrom, passingBy):
        dests = set()
        try:
            for node, directions in self.nodes[passingBy].iteritems():
                if comingFrom in directions:
                    dests.add(node)
        except KeyError:
            pass

        return dests

    def sources(self, passingBy, goingTo):
        return self.destinations(goingTo, passingBy)

This class can be used like this:

    >>> graph = Graph()
>>> graph.addEdge(('0', set([        ])), ('1', set(['3', '2'])))
>>> graph.addEdge(('1', set(['0'     ])), ('3', set(['4'     ])))
>>> graph.addEdge(('1', set(['0'     ])), ('2', set(['5'     ])))
>>> graph.addEdge(('3', set(['1', '2'])), ('4', set([        ])))
>>> graph.addEdge(('3', set(['4'     ])), ('2', set(['5'     ])))
>>> graph.addEdge(('2', set(['1', '3'])), ('5', set([        ])))

>>> print graph.isEdge('0', '1', '3')
True
>>> print graph.isEdge('1', '3', '2')
False
>>> print graph.isEdge('1', '2', '5')
True
>>> print graph.isEdge('5', '2', '3')
True
>>> print graph.isEdge('3', '2', '5')
True

>>> print graph.destinations('0', '1')
set(['3', '2'])
>>> print graph.destinations('1', '3')
set(['4'])
>>> print graph.destinations('3', '4')
set([])

>>> print graph.sources('0', '1')
set([])
>>> print graph.sources('1', '3')
set(['0'])
>>> print graph.sources('3', '4')

The chosen data structures and their usage already allows to build a directed graph, only the addEdge method would need to be adapted.

GaretJax
  • 7,462
  • 1
  • 38
  • 47