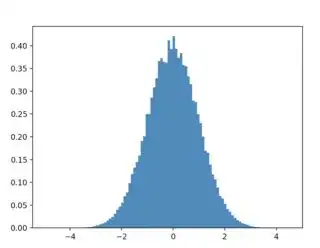
I have a Pandas DataFrame containing a dataset D of instances which all have some continuous value x. x is distributed in a certain way, say uniform, could be anything.
I want to draw n samples from D for which x has a target distribution that I can sample or approximate. This comes from a dataset, here I just take normal distribution.
How can I sample instances from D such that the distribution of x in the sample is equal/similar to an arbitrary distribution which I specify?
Right now, I sample a value x, subset D such that it contains all x +- eps and sample from that. But this is quite slow when the datasets get bigger. People must have come up with a better solution. Maybe the solution is already good but could be implemented more efficiently?
I could split x into strata, which would be faster, but is there a solution without this?
My current code, which works fine but is slow (1 min for 30k/100k, but I have 200k/700k or so.)
import numpy as np
import pandas as pd
import numpy.random as rnd
from matplotlib import pyplot as plt
from tqdm import tqdm
n_target = 30000
n_dataset = 100000
x_target_distribution = rnd.normal(size=n_target)
# In reality this would be x_target_distribution = my_dataset["x"].sample(n_target, replace=True)
df = pd.DataFrame({
'instances': np.arange(n_dataset),
'x': rnd.uniform(-5, 5, size=n_dataset)
})
plt.hist(df["x"], histtype="step", density=True)
plt.hist(x_target_distribution, histtype="step", density=True)
def sample_instance_with_x(x, eps=0.2):
try:
return df.loc[abs(df["x"] - x) < eps].sample(1)
except ValueError: # fallback if no instance possible
return df.sample(1)
df_sampled_ = [sample_instance_with_x(x) for x in tqdm(x_target_distribution)]
df_sampled = pd.concat(df_sampled_)
plt.hist(df_sampled["x"], histtype="step", density=True)
plt.hist(x_target_distribution, histtype="step", density=True)