I wrote the Extended Euclidean Algorithm, but i'm having trouble with using it to solve the following equation:

which the Modular Equation Solver reduces to
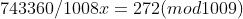
and

Here is my code:
def fastlinearcongruenceSO(powx, divmodx, N, withstats=False):
x, y, z = egcditerx2SO(powx, N, withstats)
answer = (y*divmodx)%N
if withstats == True:
print(f"answer = {answer}")
if x > 1:
powx//=x
divmodx//=x
N//=x
if withstats == True:
print(f"powx = {powx}, divmodx = {divmodx}, N = {N}")
x, y, z = egcditerx2SO(powx, N, withstats)
if withstats == True:
print(f"x = {x}, y = {y}, z = {z}")
answer = (y*divmodx)%N
if withstats == True:
print(f"answer = {answer}")
return answer
def egcditerx2SO(a, b, withstats=False):
s = 0
r = b
old_s = 1
old_r = a
quotient = 0
if withstats == True:
print(f"quotient = {quotient}, old_r = {old_r}, r = {r}, old_s = {old_s}, s = {s}")
while r!= 0:
quotient = old_r // r
old_r, r = r, old_r - quotient * r
old_s, s = s, old_s - quotient * s
if withstats == True:
print(f"quotient = {quotient}, old_r = {old_r}, r = {r}, old_s = {old_s}, s = {s}")
if b != 0:
bezout_t = quotient = (old_r - old_s * a) // b
if withstats == True:
print(f"bezout_t = {bezout_t}")
else:
bezout_t = 0
if withstats == True:
print("Bézout coefficients:", (old_s, bezout_t))
print("greatest common divisor:", old_r)
return old_r, old_s, bezout_t
To solve for inverses, i used this form:
IN: fastlinearcongruenceSO(327, 1, 1009)
OUT: 108
I'm not sure how or what changes i need to make to modify it to solve with the form of division, does anyone have any ideas of what changes i need to make or if i can solve it using my existing code? I really want to modify my code to handle it solving this equation: 743360/1008x = 272 (mod 1009) and x == 116 or for someone to let me know how that equation was solved, and i can then with those steps modify my code to solve for division based modulus equations. Thanks for anyone who knows how to solve these division based equations.