3

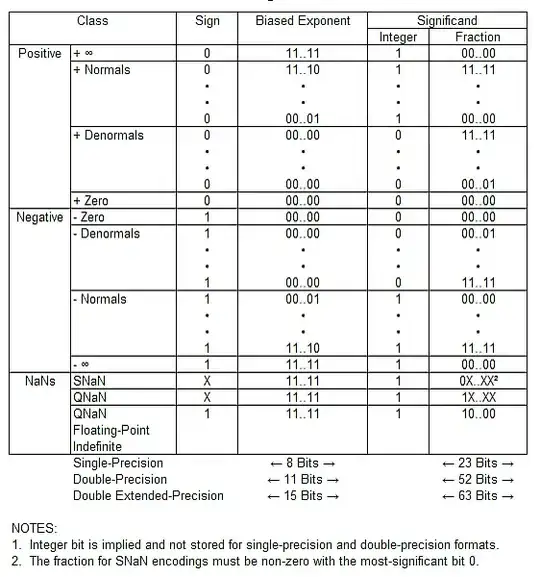
Denormal floats are something special:

floating point number classification and representation

What does the ISO-Prolog standard say on how these should be handled?

It is clear to me that raising a evaluation_error(underflow) exception whenever these denormals occur is a proper way of dealing with them, but this incurs additional costs—each float produced must be checked.

But what about the "flush denormals to zero" (FTZ) and "treat denormals as zero" (DAZ) operating modes that many processors offer? Can Prolog implementations use these, and, if so, how do they do that properly?

Does (1) documenting the use of these operating modes, (2) ensuring that denormals are flushed to zero of the same sign (FTZ), and (3) ensuring that denormals are treated as zero of the same sign (DAZ) suffice? Help please!

false
  • 10,264
  • 13
  • 101
  • 209
repeat
  • 18,496
  • 4
  • 54
  • 166
  • 2
    I would say trying to elicit wisdom about floating points from a 20+ year old standard for which floats were not a central issue, or even conforming to it is an exercise in futility, but I'm grumpy and that's just me. Even the Java standard was not appreciated by [William Kahan](https://people.eecs.berkeley.edu/~wkahan/): [How JAVA's Floating-Point Hurts Everyone Everywhere](https://people.eecs.berkeley.edu/~wkahan/JAVAhurt.pdf). _IEEE Standard 754 recommends extra-precise longdouble and over 95% desktops have it built into their hardware.You paid for it, but Java denies you its benefits._ – David Tonhofer Aug 09 '20 at 11:41
  • In particular from the above PDF: _"Invalid Operation, Overflow, Division-by-Zero, Underflow, Inexact Result" ... These events are not errors unless they are handled badly.They are called “Exceptions” because to any policy for handling them, imposed in advance upon all programmers by the computer system, some programmers will have good reasons to take exception._ – David Tonhofer Aug 09 '20 at 11:41
  • @David Tonhofer. For me, conformance is important, for I am an implementor, too. – repeat Aug 09 '20 at 14:40
  • 1
    Aside: Per IEEE, +/- 0.0 is not a subnormal (denormal) and so I would not expect FTZ, DAZ to raise _underflow_. – chux - Reinstate Monica Aug 10 '20 at 21:01
  • @chux-ReinstateMonica. I didn't mean to imply that. FTZ and DAZ are alternatives to raising the underflow. I'm just not sure if preserving the sign matters or not. – repeat Aug 10 '20 at 21:54

3 Answers3

2

Don't skip them. Yet, short answer from ISO/IEC 13211-1:1995 9.1.4.2 Floating point result function:

It shall be implementation defined whether a processor
chooses round(x) or underflow when 0 < |x| < fminN.

But first, let's call them subnormals. The obsolete (at least according to LIA 1:2012) notion denormal was (in retrospect) not very helpful as it suggested some de-viant, de-structive properties. And no: they are not special as you suggest. To see this, consider the number line of real numbers. Numbers that can be represented exactly are marked and get closer and closer to each other when approaching zero (from both sides). Subnormal are those that are closest to zero. The distance between them and zero is the same as the distance between the smallest normal numbers. That's their anomaly (or denormaly so to speak). If you remove now those subnormals you get a gigantic gap that causes even more numerical anomalies. It's like you scratch away on a ruler the markings next to zero and then use this broken ruler for measuring1. So in absence of subnormals the remaining numbers are not normal as one might believe but rather abnormal, prone to even more errors.

If you do not like to read Kahan on the subject which I nevertheless suggest, may I refer you to Gustafson's The end of error which explains subnormals much better than I do.

In 13211-1 there is the possibility to exclude subnormals but this is just for compatibility with very RISCy, outdated architectures.

So much for formal conformity. In the long term some Unum-style, CLP(BNR)-esque, Prolog IV-ish approach might be promising.

 1) That is, if you are rounding to zero. In case you produce exceptions/continuation values instead better numerical properties will hold as long as such exceptions do not occur.

false
  • 10,264
  • 13
  • 101
  • 209
2

In section 7.1.3 the ISO-Prolog standard defines the set F as the set of numbers that your chosen floating-point format can represent. This set may or may not include denormalized values, both choices are allowed.

When a computation result is (absolutely) greater than zero and smaller than the smallest normalized value, you have the choice between

  • rounding to a value representable in F
  • raising an underflow exception

According to section 9.1.4.2, this choice is implementation defined, i.e. you have to document it.

jschimpf
  • 4,904
  • 11
  • 24
0

This is a little test case to see whether your Prolog system can return subnormals as result of arithmetic (no flush-to-zero, ~FTZ):

/* SWI-Prolog */
?- X is 2.2250738585072011e-308 - 2.2250738585072012e-308.
X = -5.0e-324.
/* Jekejeke Prolog */
?- X is 2.2250738585072011e-308 - 2.2250738585072012e-308.
X = -4.9E-324

And this is a new addition in APIs, not the same across Prolog systems, showing argument passing of subnormals (no denormals-are-zero, ~DAZ):

/* SWI-Prolog */
?- X is 2.2250738585072011e-308 - 2.2250738585072012e-308, 
float_parts(X,M,B,E).
X = -5.0e-324,
M = -0.5,
B = 2,
E = -1073.
/* Jekejeke Prolog */
?- X is 2.2250738585072011e-308 - 2.2250738585072012e-308, 
sys_float_mantissa(X,M), sys_float_exponent(X,E), sys_float_radix(X,R).
X = -4.9E-324,
M = -1,
E = -1074,
R = 2

The result is from MacBook Air 2019.