Compute Renewal Process in R for Gamma distribution

Question

I am trying to find the sum for the following formula in R for alpha = 2.

I wrote the following command. How to sum from n = 1 to infinity. Please provide me a hint. Thank you in advance!

integrand <- function(x) {
  dgamma(x, shape = n * 2, rate = 1, log = FALSE)
}

integrate(integrand, lower = 0, upper = t)

Stack Overflow doesn't render LaTeX, so it's better to include an image of your LaTeX expression. I'm also not clear on what you're asking. What are you trying to do? Can you please provide some sample code and context. R provides different ways to *numerically* solve equations in R, see e.g. `uniroot`. — Maurits Evers, Aug 03 '20 at 03:11
Is this issue resolved? If so, please close the question by setting the check mark next to one of the answers. Otherwise I'm curious in hearing further details/clarifications. — Maurits Evers, Aug 08 '20 at 03:26

score 1 · Answer 1 · answered Aug 04 '20 at 23:11

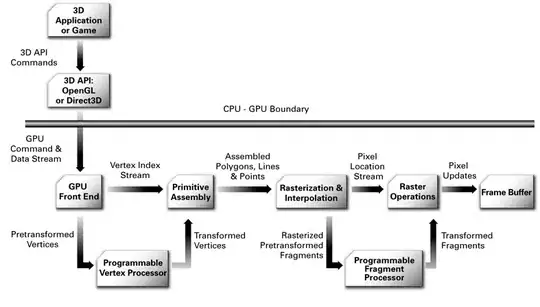
I am not really clear on what you're trying to do.

The integrand in your equation is just the probability density function (pdf) of a Gamma distribution with shape parameter k = nα and scale parameter θ = 1.

Integrating the Gamma pdf over the entire domain from 0 to infinity simply equates to 1. You can verify this numerically:

integrate(dgamma, 0, Inf, shape = 1, scale = 1)
#1 with absolute error < 5.7e-05

In the final step of your equation you sum over all values of n, from 1 to infinity. But the integral is not dependent on n, and the sum diverges

So unless I misunderstood your question, the lhs of the expression you give diverges.

score 0 · Answer 2 · answered Aug 03 '20 at 06:16

From your question n and t is missing. Also it is not entirely clear what you are trying to achieve, but integrating over any distribution is rather simple in R

x <- 1.4
f <- function(n)dgamma(x, shape = n, rate = 1, log = FALSE)
integrate(f, 0, Inf)
#Output:
1.015368 with absolute error < 0.000012

Here I integrate over the argument n, as in your equation above, while you integrated over x.

Compute Renewal Process in R for Gamma distribution

2 Answers2