MCMC Changepoint model in R

Question

I want to run an MCMC linear Gaussian Multiple Changepoint model to detect changepoints for a time-series vector of continuous values.

In doing so, I am thinking of using MCMCregressChange function, but I have several questions here:

(1) How can I obtain log marginal likelihood for these models?

(2) What is the difference between MCMCregressChange function and MCMCresidualBreakAnalysis function?

R script is shown below. I would be very pleased if you could help me solve this issue.

library(MCMCpack)
set.seed(1234)
n <- 100
x1 <- runif(n, min = 0, max  = 1)
x2 <- runif(n, min = 1, max  = 2)
X <- c(x1,x2)

B0 <- 0.1
sigma.mu=sd(X)
sigma.var=var(X)

model0 <- MCMCregressChange(X ~ 1, m=0, b0=mean(X),   mcmc=100, burnin=100, verbose = 1000,
                                   sigma.mu=sigma.mu, sigma.var=sigma.var, marginal.likelihood="Chib95")
model1 <- MCMCregressChange(X ~ 1, m=1, b0=mean(X),   mcmc=100, burnin=100, verbose = 1000,
                                   sigma.mu=sigma.mu, sigma.var=sigma.var, marginal.likelihood="Chib95")
model2 <- MCMCregressChange(X ~ 1, m=2, b0=mean(X),   mcmc=100, burnin=100, verbose = 1000,
                                   sigma.mu=sigma.mu, sigma.var=sigma.var, marginal.likelihood="Chib95")

print(BayesFactor(model0, model1, model2))

plotState(model0)
plotChangepoint(model0)

plotState(model1)
plotChangepoint(model1)

plotState(model2)
plotChangepoint(model2)

Answer 1

The "Value" subsection of the documentation describes what is returned by MCMCregressChange, stating that the log-marginal likelihood of the model is stored in the attribute logmarglike. Hence, it could be accessed like

attr(model1, "logmarglike")

These attribute values are also reported when running the line in the code:

print(BayesFactor(model0, model1, model2))

As for the difference in the models, the MCMCresidualBreakAnalysis is a special case of the MCMCregressChange, namely when the X is univariate. In fact, the code for MCMCregressChange checks if the number of columns in X is one, and if so reformats the input arguments to be a call to MCMCresidualBreakAnalysis. Since there are also no additional parameters specific to the latter, knowing MCMCregressChange is more general and all one should need to use.

Reinforcing this is a note in the MCMCresidualBreakAnalysis description:

"The code is written mainly for an internal use in testpanelSubjectBreak."

That is, while it is an exported function, it is primarily a convenience function arising from a specific use case.

Answer 2

In addition to MCMCpack, I think some Bayesian models designed particularly for changepoint detection may be useful. In R, three possible packages are bcp, mcp, and Rbeast. bcp and mcp are more versatile in terms of model fitted and data types handled. Rbeast is a method specifically for simultaneous Bayesian time series decomposition (similar to stl) and changepoint detection (similar to changepoint); Rbeast also reports posterior log marginal likelihood that can be used to compare alternative hypotheses on changepoints (speaking more precisely, for alternative priors on changepoint numbers).

Below are some quick results for your sample data with bcp and Rbeast.

set.seed(1234)
n  = 100
x1 = runif(n, min = 0, max  = 1)
x2 = runif(n, min = 1, max  = 2)
X  = c(x1,x2)

library(bcp)
fit=bcp(X)
plot(X)

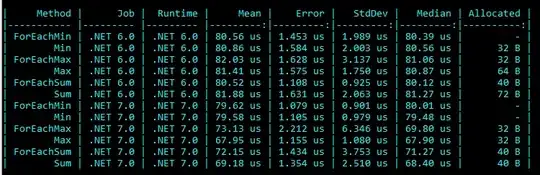
On average, bcp pinpoints roughly 2 changepoints; the best locations are indicated by the peaks in the probability curve. It can be also obtained from sum(fit$posterior.prob,na.rm = TRUE). I believe bcp here fitted piecewise constant models; the mean curve plotted above is an average of the many MCMC-sampled piecewise constant models, which gives the irregularity around the detected changepoint(s).

As a time series decomposition model, Rbeast fits a time series in the form of "Y=seasonal/periodic (if present) + trend + error". The seasonal and trend components are modelled as piecewise harmonic curves and piecewise linear (polynomials) curves, respectively. Given that there is no periodic component in the sample data, season='none' is used in the following code to fit a trend-only model. Also, as a changepoint model, Rbeast allows users to specify the range of possible numbers of changepoints; if the minimum and maximum numbers of changepoints allowed are the same and Rbeast will fix the number of changepoints to be a constant; for example, tcp.minmax=c(0,0) specifies the trend has NO changepoint. For each piecewise trend/segment, the polynomial order can be set to a range of min and max orders allowed. Below, we fix the min and max orders to zero so that we fit each segment as a constant line (i.e., torder.minmax=c(0,0)).

library(Rbeast)

model0 = beast(X, season='none', tcp.minmax = c(0,0), torder.minmax = c(0,0) ) # no changepoint
model1 = beast(X, season='none', tcp.minmax = c(1,1), torder.minmax = c(0,0) ) # 1 changepoint
model2 = beast(X, season='none', tcp.minmax = c(2,2), torder.minmax = c(0,0) ) # 2 changepoints

plot(model0)
plot(model1)
plot(model2)

# These are the posterior log marginal likelihoods; the numbers will vary slightly
# across runs due to the MCMC nature.
model0$marg_lik    #   -460.6778
model1$marg_lik    #   -313.9160 (the most likely)
model2$marg_lik)   #   -315.8801 

Below is the plot of model0 with no changepoint assumed：

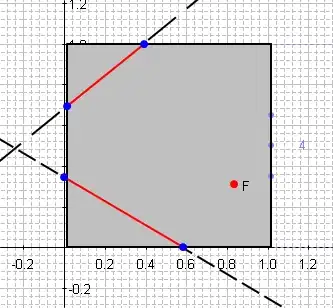
Below is the plot of model1 with only 1 changepoint specified. Note that in the prior, we just specify the numeber of changepoints to be 1 Rbeast will still find out the most likely location; it estimates its occurrence probability over time (i.e., the greeen Pr(tcp) cuvrve) plus identify the most likely location (i.e., the vertical dashed line). The order_t curves depicts the average order of the polynomial curves needed to adequately fit the trend; here it is a zero line because we fix it to zero (i.e., torder.minmax=c(0,0)).

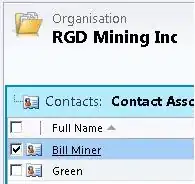
Below is a plot of model2 with 2 changepoints assumed. The estimated changepoint probability is more or less the same as the bcp result. In practice, the most reasonable way to run Rbeast is not to specify a strong prior by fixing the number of changepoints to a known constant but rather to specify a wide range and let the model figure out the numbers and locations.