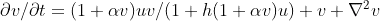RuntimeError: Factor is exactly singular (and overflow encountered in square in FiPy)

Question

I was trying to solve pde using FiPy in python. It is showing RuntimeError: Factor is exactly singular. This is not the case in these equation but in most of the equations I have computed. The equations are-

∂u/∂t = σu(1-u/C) - (1+αv)uv/(1+h(1+αv)u) +D∇^2 u and

∂v/∂t = (1+αv)uv/(1+h(1+αv)u) - v +D∇^2 v

from fipy import *
nx=ny=100
dx=dy=0.25
L=dx*nx
dt=0.01
sigma=10.0
h=0.1
C=0.8 
alp=0.57 #alpha 
mesh =Grid2D(dx=dx,dy=dy,nx=nx,ny=ny)
u=CellVariable(name='u Variable',mesh=mesh)
v=CellVariable(name='v Variable',mesh=mesh)

u.setValue(GaussianNoiseVariable(mesh=mesh,mean=0.18,variance=0.005))
v.setValue(GaussianNoiseVariable(mesh=mesh,mean=0.28,variance=0.005))

D=35
eq_u=(TransientTerm(coeff=1.0, var=u)==sigma*u*(1-v/C) -((1+alp*v)*v*u)/(1+(1+alp*v)*h*u) +ImplicitDiffusionTerm(coeff=D,var=u)) 
eq_v=(TransientTerm(coeff=1.0, var=v)==((1+alp*v)*v*u)/(1+(1+alp*v)*h*u) +v +ImplicitDiffusionTerm(coeff=1.0, var=v))

#creating viewer
if __name__ == "__main__":
    viewer_u=Viewer(vars=u,datamin=0.,datamax=1.0) 
    viewer_u.plot()
    viewer_v=Viewer(vars=v,datamin=0.,datamax=1.0)
    viewer_v.plot()

#solving
steps=50000
for step in range(steps):
    eq_u.solve(var=u,dt=dt)
    eq_v.solve(var=v,dt=dt)
    if __name__ == "__main__":
        viewer_u.plot()
        viewer_v.plot()

Error are-

C:\Users\Harshit Rathore\AppData\Local\Programs\Python\Python37-32\lib\site-packages\fipy\solvers\scipy\linearLUSolver.py:41: RuntimeWarning: invalid value encountered in double_scalars
  if (numerix.sqrt(numerix.sum(errorVector**2)) / error0)  <= self.tolerance:
C:\Users\Harshit Rathore\AppData\Local\Programs\Python\Python37-32\lib\site-packages\fipy\solvers\scipy\linearLUSolver.py:36: RuntimeWarning: overflow encountered in square
  error0 = numerix.sqrt(numerix.sum((L * x - b)**2))
C:\Users\Harshit Rathore\AppData\Local\Programs\Python\Python37-32\lib\site-packages\fipy\solvers\scipy\linearLUSolver.py:41: RuntimeWarning: overflow encountered in square
  if (numerix.sqrt(numerix.sum(errorVector**2)) / error0)  <= self.tolerance:
C:\Users\Harshit Rathore\AppData\Local\Programs\Python\Python37-32\lib\site-packages\fipy\variables\variable.py:1122: RuntimeWarning: overflow encountered in multiply
  return self._BinaryOperatorVariable(lambda a, b: a*b, other)
C:\Users\Harshit Rathore\AppData\Local\Programs\Python\Python37-32\lib\site-packages\fipy\variables\variable.py:1122: RuntimeWarning: invalid value encountered in multiply
  return self._BinaryOperatorVariable(lambda a, b: a*b, other)
Traceback (most recent call last):
  File "e:\VS_Codes\Python\V_1.py", line 32, in <module>
    eq_v.solve(var=v,dt=dt)
  File "C:\Users\Harshit Rathore\AppData\Local\Programs\Python\Python37-32\lib\site-packages\fipy\terms\term.py", line 178, in solve
    solver._solve()
  File "C:\Users\Harshit Rathore\AppData\Local\Programs\Python\Python37-32\lib\site-packages\fipy\solvers\scipy\scipySolver.py", line 26, in _solve
    self.var[:] = numerix.reshape(self._solve_(self.matrix, self.var.ravel(), numerix.array(self.RHSvector)), self.var.shape)
  File "C:\Users\Harshit Rathore\AppData\Local\Programs\Python\Python37-32\lib\site-packages\fipy\solvers\scipy\linearLUSolver.py", line 34, in _solve_
    permc_spec=3)
  File "C:\Users\Harshit Rathore\AppData\Local\Programs\Python\Python37-32\lib\site-packages\scipy\sparse\linalg\dsolve\linsolve.py", line 326, in splu
    ilu=False, options=_options)
RuntimeError: Factor is exactly singular

Is there any better pde solver in python Thankyou

score 0 · Accepted Answer · answered Jul 31 '20 at 15:20

Your FiPy code does not agree with your equations. You are solving

$\partial v/\partial t = (1+\alpha v)u v / (1 + h(1+\alpha v)u) + v + \nabla^2 v$

If I correct the FiPy code to agree with your math, then the problem runs much longer before the results diverge (which is why you get Factor is exactly singular with the scipy LU solver (other solvers have other failure modes, but all diverge)). The divergence appears to be when u or v either gets very small or negative. It's not completely clear to me as the system seems tolerant of some near-zero and negative values. It's not clear to me whether u and v should remain positive or not, but things often go badly when they don't.

Now, I would recommend making your equations more implicit, coupling them together, and sweeping, as these equations are quite non-linear and it is unlikely that the results are converged.

I'd also recommend working in 1D while you're debugging. It's easier to see what's going on.

RuntimeError: Factor is exactly singular (and overflow encountered in square in FiPy)

1 Answers1