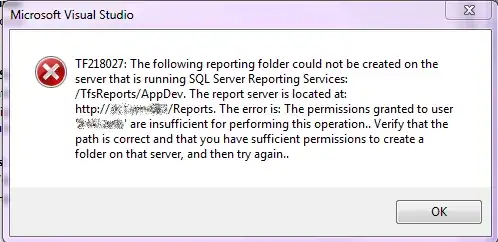
I am trying to create a scatterplot with more than the 8 default Matlab colors, but when I create a colormap I get the error: Error using set Error setting property 'MarkerFaceColor' of class 'Line': Color value must be a 3 element vector. Right now I am creating the scatterplot with:
colors = hsv(18);
gscatter3(x,y,z,idx, colors, {'.','.','.','.','.','.','.','.','.','.','.','.','.','.','.','.','.','.'},15);
I also tried manually creating a vector for the colors but still could not get anything to work other than the 8 default colors, i.e. 'b','g','r',etc. Does anyone know how to get more colors to work?