How can I express the term like diffusion term?

Question

How can I express the term like diffusion term but with a transposed matrix in FIPY?

Is \phi a vector? If not, I'm not even sure what that expression means. — jeguyer, Jul 24 '20 at 13:54

wd15 · Answer 1 · 2020-07-27T19:29:59.100

FiPy allows for general diffusion terms of the form

The coefficient requires 2x2 components in 2D or 3x3 components in 3D, but can still be spatially varying in each of those components. See the FiPy FAQ for more details.

Updated Solution

The above is not particularly useful now that I understand that 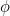$\phi$ is supposed to be a vector. Let's assume a set of equations of the form,

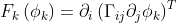
$F_k\left( \phi_k \right ) = \partial_i \left( \Gamma_{ij} \partial_j \phi_k \right )^T$

where k is not summed, but signifies the equation and particually components of 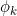$\phi_k$ being solved. That results in the following for the diffusion term,

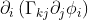
$\partial_i \left( \Gamma_{kj} \partial_j \phi_i \right )$

In your case $\Gamma_{ij} = \delta_{ij}$ . In FiPy, you'll need to represent this with multiple diffusion terms since there is more than one variable being solved for in each equation now. Assuming that we have k=x,y, only then the first equation's diffusion terms will be

eq_x = ... ==
DiffusionTerm(coeff=[[1, 0], [0, 0]], var=phi_x) + DiffusionTerm(coeff=[[0, 1], [0, 0]], var=phi_y)

The equations will then need to be combined into a single equation using eq = eq_x & eq_y

Thank you. I know the general diffusion terms, but it has a little difference. I will try again. — Xiukai Wang, Jul 25 '20 at 14:41

score 0 · Answer 2 · answered Jul 27 '20 at 19:26

I'm not seeing how to use @wd15's suggestion to use an anisotropic diffusion coefficient to achieve transposition.

Working my slow wits through Einstein notation, it looks to me like:

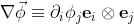
$\nabla\vec{\phi} \equiv \partial_i\phi_j\mathbf{e}_i\otimes \mathbf{e}_j$

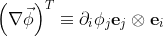
$\left( \nabla\vec{\phi}\right )^T \equiv \partial_i\phi_j\mathbf{e}_j\otimes \mathbf{e}_i$

$\begin{aligned}\nabla\cdot\left( \nabla\vec{\phi}\right )^T &\equiv \nabla\cdot\left(\partial_i\phi_j\mathbf{e}_j\otimes \mathbf{e}_i \right ) \\ &=\left[\nabla\cdot\left(\partial_i\phi_j\mathbf{e}_j \right ) \right ]\mathbf{e}_i +\partial_i\phi_j\mathbf{e}_j\cdot\nabla\mathbf{e}_i \\ &=\left[\partial_k\mathbf{e}_k\left(\partial_i\phi_j\mathbf{e}_j \right ) \right ]\mathbf{e}_i \\ &=\left(\partial_j\partial_i\phi_j \right )\mathbf{e}_i \\ &=\partial_i\left(\partial_j\phi_j \right )\mathbf{e}_i \\ &\equiv \nabla\left(\nabla\cdot\vec{\phi} \right ) \end{aligned}$

Maybe that's an obvious result, but it wasn't obvious to me.

FiPy doesn't have a Term that represents this, so I think you'll just need to calculate it explicitly, e.g.

grad_div_phi = phi.divergence.grad
u_eq = TransientTerm(...) == ... + grad_div_phi.dot([1, 0, 0])
v_eq = TransientTerm(...) == ... + grad_div_phi.dot([0, 1, 0])
w_eq = TransientTerm(...) == ... + grad_div_phi.dot([0, 0, 1])

If @wd15 agrees with my interpretation of this term, he may see a more implicit way to incorporate it into your equation.

I think that the maths is equivalent to my answer so the implicit formulation stated above will work. Also possible to not have coupled equations but have one part implicit and one part explicit. — wd15, Jul 27 '20 at 19:43
Thank you for your help. It helped me a lot. Wish you have a nice day. — Xiukai Wang, Jul 29 '20 at 00:36

How can I express the term like diffusion term?

2 Answers2

Updated Solution