I am reading a statistics textbook Introduction to Statistics for Engineers by Sheldon Ross, p.275 and trying to re-do its examples on paper and in Octave. I am not able to replicate many Bayes calculations in Octave when it comes to the integration part. Please advise how to go about replicating below calculation in Octave? Below is a simple Bayes estimator example which naturally becomes a symbolic integration problem, where I often encounter difficulty doing in Octave.
[Clarification: This calculation is from a textbook and I understand it by hand. What I don't understand is how should one approach such statistical computing exercises in practice. This question relates to statistical/scientific computing, not coding or statistics per se.]
Suppose  are independent Bernoulli variables, having pdf
are independent Bernoulli variables, having pdf 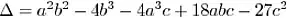
p is the unknown variable  .
Compute the Bayes estimator for p.
.
Compute the Bayes estimator for p.
The conditional pdf of p given X is then
Using (1) and letting  , the conditional pdf becomes
, the conditional pdf becomes
Therefore, Bayes estimator for p is:
Now, I try to replicate these steps using Octave as below and failed (integration took 40mins on my $2500 Dell desktop). Can you show my confused soul how do you do the above steps in Octave or Matlab or R to arrive at the same Bayes estimator?
#Use Octave to derive the above Bayes estimator
pkg load symbolic;
syms p n x;
f = (p^x) * (1-p)^(n-x);
F = int(f, p, [0, 1]); #integrate f, which gives the conditional pdf denominator
f_conditional = f/F; #the conditional pdf
integrand = p * f_conditional; # the integrand to derive Bayes estimator
estimator = int(integrand, p, [0, 1]);
#this integration takes forever, how else should I replicate the above in Octave?