I use MATH.NET implementation of Kalman Filter
My example is similar to example described in this very useful manual:
Consider a truck on frictionless, straight rails. Initially, the truck is stationary at position 0, but it is buffeted this way and that by random uncontrolled forces. We measure the position of the truck every Δt seconds, but these measurements are imprecise; we want to maintain a model of the truck's position and velocity.
The position and velocity of the truck are described by the linear state space
where x' is the velocity, that is, the derivative of position with respect to time.
Math details can be found by the mentioned link.
Finally, I have this very simple .NET implementation with 2 filter parameters (_measurementCovariance and _plantNoiseVar):
//set up filter
var xState = Matrix<double>.Build.Dense(2, 1, new[] { x0, v0 });
var measurementCovarianceMatrix = Matrix<double>.Build.Dense(2, 2,
new[] { _measurementCovariance, _measurementCovariance / dt,
_measurementCovariance / dt, 2 * _measurementCovariance / (dt * dt) });
_dkf = new DiscreteKalmanFilter(xState, measurementCovarianceMatrix);
_stateTransitionMatrixF = Matrix<double>.Build.Dense(2, 2, new[] { 1d, 0d, dt, 1 });
_plantNoiseMatrixG = Matrix<double>.Build.Dense(2, 1, new[] { (dt * dt) / 2, dt});
_plantNoiseVarianceQ = (_plantNoiseMatrixG.Transpose() * _plantNoiseMatrixG) * _plantNoiseVar;
_measurementVarianceMatrixR = Matrix<double>.Build.Dense(1, 1, new[] { _measurementCovariance });
_measurementMatrixH = Matrix<double>.Build.Dense(1, 2, new[] { 1d, 0d });
//update function
private void Update(double newPosition, double dt)
{
var z = Matrix<double>.Build.Dense(1, 1, new[] { newPosition });
_stateTransitionMatrixF[0, 1] = dt;
_plantNoiseMatrixG[0, 0] = (dt* dt) / 2;
_plantNoiseMatrixG[1, 0] = dt;
_dkf.Predict(_stateTransitionMatrixF, _plantNoiseMatrixG, _plantNoiseVarianceQ);
_dkf.Update(z, _measurementMatrixH, _measurementVarianceMatrixR);
}
Then I tested this implementation for real data I have:
For each X position I invoked Update function and stored Kalman Velocity prediction via:
kalmanPosition = _dkf.State[0, 0];
kalmanVelocity = _dkf.State[1, 0];
kalmanSpeedInstant = (kalmanPosition - _prevPosition) / dt;
_prevPosition = kalmanPosition;
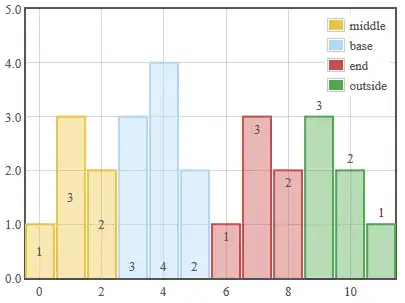
Here is a plot with results:
What I cannot understand, why Kalman speed is so small for my example. Can anyone please help me with this example.
- Do I interpret results correctly?
- Is this _dkf.State[1, 0] a speed, or am I wrong with that?
- Were there any mistakes in my assumptions?
- How can I get more accurate speed?
I used the parameters:
_measurementCovariance = 1.5 and _plantNoiseVar = 3.0.
Data I used:
new[] //positions { -0.05, -0.04, -0.04, -0.03, -0.03, -0.03, -0.03, -0.03, -0.02, -0.01, 0, 0.06, 0.07, 0.03, 0.01, 0.02, 0.04, 0.04, 0.05, 0.06, 0.07, 0.08, 0.1, 0.11, 0.12, 0.12, 0.14, 0.15, 0.15, 0.17, 0.18, 0.2, 0.21, 0.25, 0.28, 0.3, 0.35, 0.44, 0.48, 0.56, 0.6, 0.63, 0.67, 0.71, 0.71, 0.73, 0.75, 0.76, 0.79, 0.81, 0.82, 0.88, 1.13, 1.16, 1.16, 1.15, 1.16, 1.19, 1.2, 1.24, 1.26, 1.29, 1.34, 1.66, 1.52, 1.69, 2.04, 2.05, 2.08, 2.12, 2.16, 2.21, 2.28, 2.33, 2.38, 2.45, 2.5, 2.54, 2.59, 2.65, 2.7, 2.76, 2.93, 3.15, 3.23, 3.28, 3.35, 3.41, 3.48, 3.55, 3.46, 3.52, 3.75, 3.83, 3.92, 3.99, 4.08, 4.15, 4.22, 4.31, 4.54, 4.8, 4.99, 5.08, 5.14, 5.22, 5.44, 5.51, 5.55, 5.63, 5.71, 5.8, 5.88, 5.97, 6.06, 6.16, 6.49, 6.57, 6.65, 6.73, 6.82, 6.9, 7.01, 7.16, 7.25, 7.34, 7.42, 7.52, 7.62, 7.71, 7.81, 7.91, 8.01, 8.32, 8.39, 8.47, 8.68, 8.73, 8.78, 8.86, 8.95, 9.24, 9.21, 9.3, 9.4, 9.49, 9.59, 9.7, 9.79, 9.89, 9.99, 10.27, 10.37, 10.29, 10.38, 10.48, 10.58, 10.69, 10.78, 10.87, 10.98, 11.06, 11.15, 11.24, 11.44, 11.54, 11.63, 11.74, 11.84, 11.94, 12.05, 12.17, 12.28, 12.39, 12.48, 12.6, 12.69, 12.8, 12.92, 13.01, 13.11, 13.21, 13.31, 13.52, 13.62, 13.72, 13.83, 13.94, 14.05, 14.15, 14.47, 14.58, 14.69, 14.8, 14.91, 15.02, 15.12, 15.22, 15.33, 15.42, 15.52, 15.62, 15.72, 15.93, 16.03, 16.14, 16.24, 16.36, 16.47, 16.59, 16.71, 16.83, 16.94, 17.06, 17.17, 17.28, 17.4, 17.5, 17.61, 17.72, 17.82, 17.93, 18.04, 18.15, 18.26, 18.37, 18.49, 18.6, 18.71, 19.11, 19.26, 19.17, 19.29, 19.4, 19.51, 19.68, 19.75, 19.96, 20.05, 20.1, 20.28, 20.35, 20.47, 20.57, 20.84, 20.91, 21.28, 21.41, 21.52, 21.64, 21.74, 21.9, 21.99, 22.78, 22.9, 23, 23.12, 23.24, 23.36, 23.48, 23.61, 23.74, 23.98, 24.1, 24.2, 24.31, 24.42, 24.53, 24.63, 24.75, 24.86, 24.97, 25.09, 25.21, 25.34, 25.45, 25.59, 25.71, 25.82, 25.95, 26.07, 26.18, 26.31, 26.42, 26.54, 26.65, 26.76, 26.88, 27, 27.12, 27.24, 27.37, 27.49, 27.61, 27.74, 27.85, 27.97, 28.08, 28.19, 28.3, 28.41, 28.52, 28.75, 29, 29.12, 29.24, 29.36, 29.49, 29.62, 29.75, 29.88, 30.02, 30.15, 30.26, 30.37, 30.5, 30.71, 30.82, 30.92, 31.02, 31.11, 31.22, 31.33, 31.44, 31.54, 31.63, 31.73, 31.84, 31.97, 32.06, 32.17, 32.26, 32.38, 32.49, 32.61, 32.76, 32.92, 34.05, 34.13, 34.62, 34.69, 34.75, 34.83, 34.92, 35, 35.1, 35.19, 35.29, 35.4, 35.51, 35.6, 35.72, 35.82, 35.93, 36.23, 36.39, 36.54, 39.18, }
new[] //time { 0, 0.17, 0.2, 0.23, 0.24, 0.25, 0.27, 0.28, 0.31, 0.32, 0.33, 0.35, 0.36, 0.37, 0.39, 0.4, 0.41, 0.43, 0.44, 0.45, 0.47, 0.48, 0.49, 0.51, 0.52, 0.53, 0.55, 0.56, 0.57, 0.59, 0.6, 0.61, 0.63, 0.64, 0.65, 0.67, 0.68, 0.69, 0.71, 0.72, 0.73, 0.75, 0.76, 0.77, 0.79, 0.8, 0.81, 0.83, 0.84, 0.85, 0.87, 0.88, 0.96, 0.97, 0.99, 1, 1.01, 1.03, 1.04, 1.05, 1.07, 1.08, 1.09, 1.11, 1.12, 1.13, 1.23, 1.25, 1.27, 1.28, 1.29, 1.31, 1.32, 1.33, 1.35, 1.36, 1.37, 1.39, 1.4, 1.41, 1.43, 1.44, 1.45, 1.47, 1.48, 1.49, 1.51, 1.52, 1.53, 1.55, 1.56, 1.6, 1.64, 1.65, 1.67, 1.68, 1.69, 1.71, 1.72, 1.73, 1.75, 1.77, 1.81, 1.83, 1.84, 1.85, 1.92, 1.93, 1.95, 1.96, 1.97, 1.99, 2, 2.01, 2.03, 2.04, 2.09, 2.11, 2.12, 2.13, 2.15, 2.16, 2.17, 2.2, 2.21, 2.23, 2.24, 2.25, 2.27, 2.28, 2.29, 2.31, 2.32, 2.36, 2.37, 2.39, 2.4, 2.41, 2.43, 2.44, 2.45, 2.48, 2.49, 2.51, 2.52, 2.53, 2.55, 2.56, 2.57, 2.59, 2.6, 2.61, 2.63, 2.64, 2.65, 2.67, 2.68, 2.69, 2.71, 2.72, 2.73, 2.75, 2.76, 2.77, 2.8, 2.81, 2.83, 2.84, 2.85, 2.87, 2.88, 2.89, 2.91, 2.92, 2.93, 2.95, 2.96, 2.97, 2.99, 3, 3.01, 3.03, 3.04, 3.07, 3.08, 3.09, 3.11, 3.12, 3.13, 3.15, 3.19, 3.2, 3.21, 3.23, 3.24, 3.25, 3.27, 3.28, 3.29, 3.31, 3.32, 3.33, 3.35, 3.37, 3.39, 3.4, 3.41, 3.43, 3.44, 3.45, 3.47, 3.48, 3.49, 3.51, 3.52, 3.53, 3.55, 3.56, 3.57, 3.59, 3.6, 3.61, 3.63, 3.64, 3.65, 3.67, 3.68, 3.69, 3.71, 3.73, 3.75, 3.76, 3.77, 3.79, 3.8, 3.81, 3.83, 3.85, 3.87, 3.88, 3.89, 3.91, 3.92, 3.93, 3.96, 3.97, 4.01, 4.03, 4.04, 4.05, 4.07, 4.08, 4.09, 4.19, 4.2, 4.21, 4.23, 4.24, 4.25, 4.27, 4.28, 4.29, 4.32, 4.33, 4.35, 4.36, 4.37, 4.39, 4.4, 4.41, 4.43, 4.44, 4.45, 4.47, 4.48, 4.49, 4.51, 4.52, 4.53, 4.55, 4.56, 4.57, 4.59, 4.6, 4.61, 4.63, 4.64, 4.65, 4.67, 4.68, 4.69, 4.71, 4.72, 4.73, 4.75, 4.76, 4.77, 4.79, 4.8, 4.81, 4.83, 4.84, 4.87, 4.89, 4.91, 4.92, 4.93, 4.95, 4.96, 4.97, 4.99, 5, 5.01, 5.03, 5.04, 5.05, 5.08, 5.09, 5.11, 5.12, 5.13, 5.15, 5.16, 5.17, 5.19, 5.2, 5.21, 5.23, 5.24, 5.25, 5.27, 5.28, 5.29, 5.31, 5.32, 5.33, 5.35, 5.48, 5.49, 5.57, 5.59, 5.6, 5.61, 5.63, 5.64, 5.65, 5.67, 5.68, 5.69, 5.71, 5.72, 5.73, 5.75, 5.76, 5.79, 5.8, 5.81, 7.23, });