Rebuilding original signal from frequencies, amplitude, and phase obtained after doing an fft.
Greetings
I'm trying to rebuild a signal from the frequency, amplitude, and phase obtained after I do an fft of a signal, but when I try and combine the fft data (frequency, amplitude, and phase) back to see if I get a similar signal, the pattern is a little off. I think it has to do with my formula which may be a little incorrect.
The formula I'm using to combine the data is:
amplitude*sin(2*pi*time*frequency+phase)+amplitude*cos(2*pi*time*frequency+phase);
Please note: At the moment I don't want to use IFFT due to the fact that I will be editing the amplitude and frequencies before the calculations are done
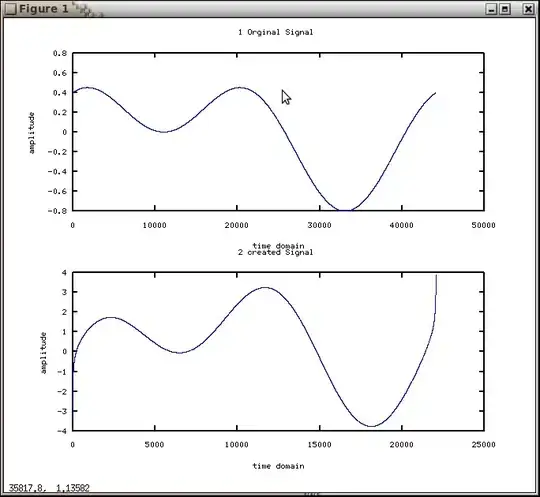
An image of the plot is below. The top one is the original signal and the bottom one is the signal created with the equation. If you want to know I'm using matlab but I think the problem is with the equation.
tia