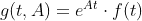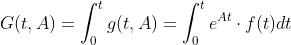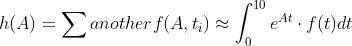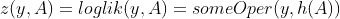Yes, you can use tensorflow GradientTape to work out the gradients. I assume you have a mathematical function outputting log_lik with many inputs, one of it is A
GradientTape to get the gradient of A
The get the gradients of log_lik with respect to A, you can use the tf.GradientTape in tensorflow
For example:
with tf.GradientTape(persistent=True) as g:
g.watch(A)
t = tf.linspace(0., 10., 100)
f = tf.ones(100)
delta = t[1]-t[0]
sum_term = tfm.multiply(tfm.exp(A*t), f)
integrals = 0.5*delta*tfm.cumsum(sum_term[:-1] + sum_term[1:], axis=0)
pred = integrals
sq_diff = tfm.square(observed_data - pred)
sq_diff = tf.reduce_sum(sq_diff, axis=0)
log_lik = -0.5*tfm.log(2*PI*variance) - 0.5*sq_diff/variance
z = log_lik
## then, you can get the gradients of log_lik with respect to A like this
dz_dA = g.gradient(z, A)
dz_dA contains all partially derivatives of variables in A
I just show you the idea by the code above. In order to make it works you need to do the calculation by Tensor operation. So change to modify your function to use tensor type for the calculation
Another example but in tensor operation
x = tf.constant(3.0)
with tf.GradientTape() as g:
g.watch(x)
with tf.GradientTape() as gg:
gg.watch(x)
y = x * x
dy_dx = gg.gradient(y, x) # Will compute to 6.0
d2y_dx2 = g.gradient(dy_dx, x) # Will compute to 2.0
Here you can see more example from the document to understand more https://www.tensorflow.org/api_docs/python/tf/GradientTape
Further discussion on "meaningfulness"
Let me translate the python code to mathematics first (I use https://www.codecogs.com/latex/eqneditor.php, hope it can display properly):
# integrate e^At * f[t] with respect to t between 0 and t, for all t
From above, it means you have a function. I call it g(t, A)
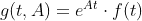
Then you are doing a definite integral. I call it G(t,A)
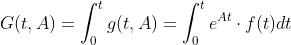
From your code, t is not variable any more, it is set to 10. So, we reduce to a function that has only one variable h(A)

Up to here, function h has a definite integral inside. But since you are approximating it, we should not think it as a real integral (dt -> 0), it is just another chain of simple maths. No mystery here.
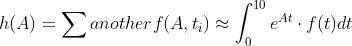
Then, the last output log_lik, which is simply some simple mathematical operations with one new input variable observed_data, I call it y.
Then a function z that compute log_lik is:
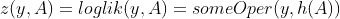
z is no different than other normal chain of maths operations in tensorflow. Therefore, dz_dA is meaningful in the sense that the gradient of z w.r.t A gives you the gradient to update A that you can minimize z