Scalar Multiplication on Elliptic Curves

Question

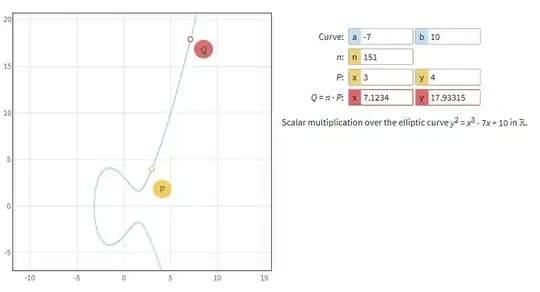
I use this article for my task https://andrea.corbellini.name/2015/05/17/elliptic-curve-cryptography-a-gentle-introduction/

Scalar multiplication is

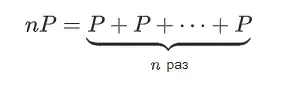
where n is a natural number

I use this code for finding Q


    import numpy as np
    def f(x,a,b):
        return x**3+a*x + b

    def bits(n):
        while n:
            yield n & 1
            n >>= 1

    def double_and_add(n, x):
        result = 0
        addend = x

        for bit in bits(n):
            if bit == 1:
                result += addend
            addend *= 2

        return result



    P = 3
    Q = double_and_add(P,151)  #453  <--- issue here

    xp = P
    yp = np.sqrt(f(xp)) #4 

    xq = Q
    yq = np.sqrt(f(xq))

Why my Q variable not matched with variable on site https://cdn.rawgit.com/andreacorbellini/ecc/920b29a/interactive/reals-mul.html

One Lyner · Accepted Answer · 2020-05-18T12:08:03.500

3

The article is misleading, because the double_and_add function is written for numbers, not points.

P should be a point, i.e the tuple (3,4).

You must then implement the group law. You can use the Algebraic addition formulas from you reference:

a, b = -7, 10  # curve coefficients from your exemple

def add(P, Q):
    if P is None or Q is None: # check for the zero point 
        return P or Q
    xp, yp = P
    xq, yq = Q
    if xp == xq:
        return double(P)
    m = (yp - yq) / (xp - xq)
    xr = m**2 - xp - xq
    yr = yp + m * (xr - xp)
    return (xr, -yr)

def double(P): 
    if P is None:
        return None 
    xp, yp = P 
    m = (3 * xp ** 2 + a) / (2 * yp) 
    xr = m**2 - 2*xp 
    yr = yp + m * (xr - xp) 
    return (xr, -yr)

In your double_and_add, use the group low for addition and doubling.

def double_and_add(n, P):
    result = None # This is our zero point
    addend = P
    for b in bits(n):
        if b:
            result = add(result, addend)
        addend = double(addend)
    return result

And you can verify:

> double_and_add(151, (3,4))
(7.12340267635097, 17.93315495174943)

edited May 18 '20 at 12:08

answered May 17 '20 at 12:54

One Lyner

1,964
1
6
8

i have multiply operation, not adding – user1088259 May 17 '20 at 15:09
What do you think means `add` in `double_and_add` ? – One Lyner May 18 '20 at 09:49
your code make `Algebraic addition`, but i need `Scalar multiplication` – user1088259 May 18 '20 at 11:10
in my code `add` does an addition, `double_and_add` does a scalar multiplication – One Lyner May 18 '20 at 11:34
`double` - what makes this function? – user1088259 May 18 '20 at 11:51
it's the addition in the case where `P == Q`. `2P` is double P. It's needed because in the other addition formula you divide by `xp - xq` which would be `0` if `P == Q`. – One Lyner May 18 '20 at 12:04

Scalar Multiplication on Elliptic Curves

1 Answers1