Optimizing a Summation function - GEKKO

Question

I just started learning optimization and I have some issues finding the optimal value for the problem below. Note: This is just a random problem that came to my mind and has no real application.

Problem:

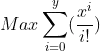
where x can be any value from the list ([2,4,6]) and y is between 1 and 3.

My attempt:

from gekko import GEKKO
import numpy as np
import math

def prob(x,y,sel):
    z = np.sum(np.array(x)*np.array(sel))
    cst = 0
    i=0
    while i <= y.VALUE:
        fact = 1
        for num in range(2, i + 1): # find the factorial value
            fact *= num
        cst += (z**i)/fact
        i+=1
    return cst


m = GEKKO(remote=False)

sel = [2,4,6] # list of possible x values
x =  m.Array(m.Var, 3, **{'value':1,'lb':0,'ub':1, 'integer': True})
y = m.Var(value=1,lb=1,ub=3,integer=True)

# switch to APOPT
m.options.SOLVER = 1

m.Equation(m.sum(x) == 1) # restrict choice to one selection

m.Maximize(prob(x,y,sel))
m.solve(disp=True)


print('Results:')
print(f'x: {x}')
print(f'y : {y.value}')
print('Objective value: ' + str(m.options.objfcnval))

Results:

----------------------------------------------------------------
 APMonitor, Version 0.9.2
 APMonitor Optimization Suite
 ----------------------------------------------------------------


 --------- APM Model Size ------------
 Each time step contains
   Objects      :  0
   Constants    :  0
   Variables    :  4
   Intermediates:  0
   Connections  :  0
   Equations    :  2
   Residuals    :  2

 Number of state variables:    4
 Number of total equations: -  1
 Number of slack variables: -  0
 ---------------------------------------
 Degrees of freedom       :    3

 ----------------------------------------------
 Steady State Optimization with APOPT Solver
 ----------------------------------------------
Iter:     1 I:  0 Tm:     -0.00 NLPi:    2 Dpth:    0 Lvs:    0 Obj: -7.00E+00 Gap:  0.00E+00
 Successful solution

 ---------------------------------------------------
 Solver         :  APOPT (v1.0)
 Solution time  :  0.024000000000000004 sec
 Objective      :  -7.
 Successful solution
 ---------------------------------------------------


Results:
x: [[0.0] [0.0] [1.0]]
y : [1.0]
Objective value: -7.0

x should be [0,0,1] (i.e. 6) and y should be 3 to get the maximum value (61). x value I get is correct but for some reason the y value I get is wrong. What is causing this issue ? Is there something wrong with my formulation ? Also it would be very helpful if you could kindly point me towards more information about the various notations (like Tm, NLPi, etc) in APOPT solver output.

Answer 1

Here is a solution in gekko:

x=6.0
y=3.0

You'll need to use the gekko functions to build the functions and pose the problem in a way so that the equations don't change as the variable values change.

from gekko import GEKKO
import numpy as np
from scipy.special import factorial

m = GEKKO(remote=False)
x = m.sos1([2,4,6])
yb = m.Array(m.Var,3,lb=0,ub=1,integer=True)
m.Equation(m.sum(yb)==1)
y = m.sum([yb[i]*(i+1) for i in range(3)])
yf = factorial(np.linspace(0,3,4))
obj = x**0/yf[0]
for j in range(1,4):
    obj += x**j/yf[j]
    m.Maximize(yb[j-1]*obj)
m.solve()
print('x='+str(x.value[0]))
print('y='+str(y.value[0]))
print('Objective='+str(-m.options.objfcnval))

For your problem, I used a Special Ordered Set (type 1) to get the options of 2, 4, or 6. To select y as 1, 2, or 3 I calculated all possible values and then used a binary selector yb to choose one. There is a constraint that only one of them can be used with m.sum(yb)==1. There are gekko examples, documentation, and a short course available if you need additional resources. Here is the solver output:

 ----------------------------------------------------------------
 APMonitor, Version 0.9.2
 APMonitor Optimization Suite
 ----------------------------------------------------------------


 --------- APM Model Size ------------
 Each time step contains
   Objects      :  1
   Constants    :  0
   Variables    :  11
   Intermediates:  1
   Connections  :  4
   Equations    :  10
   Residuals    :  9

 Number of state variables:    11
 Number of total equations: -  7
 Number of slack variables: -  0
 ---------------------------------------
 Degrees of freedom       :    4

 ----------------------------------------------
 Steady State Optimization with APOPT Solver
 ----------------------------------------------
Iter:     1 I:  0 Tm:      0.00 NLPi:    6 Dpth:    0 Lvs:    0 Obj: -6.10E+01 Gap:  0.00E+00
 Successful solution

 ---------------------------------------------------
 Solver         :  APOPT (v1.0)
 Solution time  :  0.047799999999999995 sec
 Objective      :  -61.
 Successful solution
 ---------------------------------------------------


x=6.0
y=3.0
Objective=61.0

Here is more information on the solver APOPT options. The iteration summary describes the branch and bound progress. It is Iter=iteration number, Tm=time to solve the NLP, NLPi=NLP iterations, Dpth=depth in the branching tree, Lvs=number of candidates leaves, Obj=NLP solution objective, and Gap=gap between integer solution and best non-integer solution.

Answer 2

equation to be minimzedhey how to solve these type of prolems

problem:

Minimization

summation(xij*yij)

i=from 0 to 4000 j= from 0 to 100

y is coast matrix given

m = GEKKO(remote=False)
dem_var = m.Array(m.Var,(4096,100),lb=0)

for i,j in s_d:
   m.Minimize(sum([dem_var[i][j]*coast_new[i][j]]))

here y=coast_new x= dem_var