There might be an answer for that floating around somewhere but I wasn't able to find it.
I want to minimize 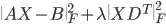 with variable
with variable X >= 0 and 1st derivative matrix D, so that X is smooth in column-direction and with relatively large data.
In the past I have used various ways of solving this (e.g. with scipy.optimize.lsq_linear or pylops) and now wanted to try out cvxpy with the generic approach below (using SCS, because the problem wouldn't fit into memory otherwise):
def cvxpy_solve_smooth(A, B, lambd=0):
D = get_D(B.shape[1])
X = cp.Variable((A.shape[1], B.shape[1]))
cost1 = cp.sum_squares(A @ X - B)
cost2 = lambd * cp.sum_squares(X @ D.T)
constr = [0 <= X]
prob = cp.Problem(cp.Minimize(cost1 + cost2), constr)
prob.solve(solver=cp.SCS)
return X.value
def get_D(n):
D = np.diag(np.ones(n - 1), 1)
np.fill_diagonal(D, -1)
D = D[:-1]
return D
However, this is considerably slower than scipy.optimize.lsq_linear with sparse matrices. What can I do in terms of problem formulation, solver options, cvxpy advanced features etc. to improve performance?