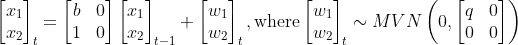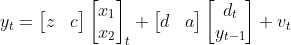Estimation of a state-space model with lags in the measurement equation in R

Question

I'm trying to estimate an SS model from this paper that has the following form:

$\pi_t=\alpha(L)\pi_{t-1}-\beta(L)(u_t-u_t^*)+\gamma(L)z_t+\epsilon_t\u_t^*=u_{t-1}^*+\eta_t$

Setting the order of the first lag polynomial to zero and the second one to one, we can reformulate it using terms from the MARSS package guide when applicable (x is the state, y is the observed variable, d is exogenous):

$y_t=Zx_{t}+Dd_t+Ay_{t-1}+Cx_{t-1}+v_t\x_t=Bx_{t-1}+w_t$

MARSS package allows for estimation of a simpler model that dooesn't include lagged variables in the measurement equation. Is there a way to estimate this one using MARSS or any other package without rewriting the estimation routine for this special case? Maybe there is a way to reformulate it so it could be "fed" to MARSS or some other package?

Eli Holmes · Accepted Answer · 2020-07-14T16:06:33.250

Take a look at how say the BSM Structural time series model or ARMA model is formulated as a MARSS model, aka a multivariate state-space model. That'll give you an idea of how to reform your model in multivariate state-space form.

Basically, your x will look like

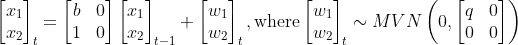
$\begin{bmatrix}x_1\\x_2\end{bmatrix}_{t}=\begin{bmatrix}b&0\\1&0\end{bmatrix}\begin{bmatrix}x_1\\x_2\end{bmatrix}_{t-1}+\begin{bmatrix}w_1\\w_2\end{bmatrix}_{t}, \text{where} \begin{bmatrix}w_1\\w_2\end{bmatrix}_{t} \sim MVN\left(0,\begin{bmatrix}q&0\\0&0\end{bmatrix}\right)$

See how the x_2 is just a dummy that is forced to be x(t-1)?

Now the y equation

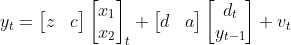
$y_{t}=\begin{bmatrix}z&c\end{bmatrix}\begin{bmatrix}x_1\\x_2\end{bmatrix}_{t}+\begin{bmatrix}d&a\end{bmatrix}\begin{bmatrix}d_t\\y_{t-1}\end{bmatrix}+v_{t}$

The d and a are your D and A. I wrote in small case to spec that they are scalars. But they can be matrices in general (if y is multivariate say). Your inputs are the d_t and y_{t-1}. You prepare that 2x1xT matrix as an input.

Be careful with your initial condition specification. Probably best/easiest to set it at t=1 and estimate or use diffuse prior.

You can fit this model with MARSS. You can fit with any Kalman filter function that will allow you to pass in inputs in the y equation (some do, some don't). KFAS::KFS() allows that using the SScustom() function.

In MARSS the model list will look like so

mod.list=list(
B=matrix(list("b",1,0,0),2,2),
U=matrix(0,2,1),
Q=matrix(list("q",0,0,0),2,2),
Z=matrix(c("z", "c"),1,2),
A=matrix(0),
R=matrix("r"),
D=matrix(c("d", "a"),1,2),
x0=matrix(c("x1","x2"),2,1),
tinitx=1,
d=rbind(dt[2:TT],y[1:(TT-1)])
)
dat <- y[2:TT] # since you need y_{t-1} in the d (inputs)
fit <- MARSS(dat, model=mod.list)

It'll probably complain that it wants initial conditions for x0. Anything will work. The EM algorithm isn't sensitive to that like a BFGS or Newton algorithm. But method="BFGS" is actually often better for this type of structural ts model and in that case pick a reasonable initial condition for x (reasonable = close to your data in this case I think).

Estimation of a state-space model with lags in the measurement equation in R

1 Answers1