Passing large time dependent data to solve differential equation in python,

Question

Consider this simple first-order differential equation:

Where k is a constant with value 0.5 and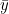 is a variable that changes with time.

I used the following code to input the values of y_bar at different times which works perfectly.

import numpy as np
from scipy.integrate import odeint
from matplotlib import pyplot as plt
def get_y_bar(t):
    if t>=0 and t<=1:
        return 0.0
    elif t<=2:
        return 1.0
    elif t<=3:
        return 2.0
    elif t<=4:
        return 3.0
    elif t<=5:
        return 4.0
    else:
        return 5.0
def ode(y,t):
    k=0.5
    y_bar=get_y_bar(t)
    dy=k*(y_bar-y)
    return dy
y0=0.0
t0=np.linspace(0,10,100)
sol=odeint(ode,y0,t0)
plt.plot(t0,sol)
plt.show() 

But, this method is feasible only when I have a small data and can enter it using if.. elif..else loop manually. What can I do if I have large values of y_bar in smaller time steps (eg, t= 0.01, 0.025, 0.03,..., 5.0)??

I have the data in CSV format and tried looping through the data but got stuck !! Is there any simple way to do this??

def get_y_bar(t):
    data=np.genfromtxt('data.csv',delimiter=',')
    time=data[:,0]
    y_bar=data[:,1]
    for i in range(len(time)):
        if t>=time[i] and t<=time[i=1]:
            return y_bar[i]
        else:

Answer 1

I am not sure if I understood your question completely. But if you want to replace the numerous elif loops in get_y_bar, try this:

import math

def get_y_bar(t):
    return math.floor(t)

That is, math.floor(4.2) will return 4, which is the largest integer smaller than 4.2

Answer 2

With that approach you would load your file every time odeint does a call to your ode function, which will be highly inefficient.

A more convenient way to solve your problem is to replace your get_y_bar function by using scipy.interpolate.interp1d instead, with kind = zero, i.e. constant interpolation. You should do this interpolation outside of your ode function, so you only do it once.