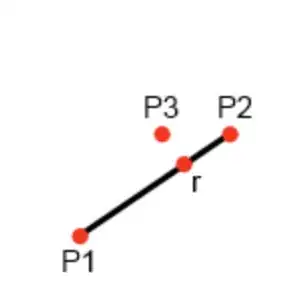
If i have three points P1, P2, P3 with their coordinates(x,y)
P1(x,y) and P3(x,y) are coordinate of line(start, end) and P3 is a point need to be projected.
how can i find the coordinate of point r(x,y) which is projection of P3 over P1 and P2
If i have three points P1, P2, P3 with their coordinates(x,y)
P1(x,y) and P3(x,y) are coordinate of line(start, end) and P3 is a point need to be projected.
how can i find the coordinate of point r(x,y) which is projection of P3 over P1 and P2

This solution extends to points with any geometric dimensions (2D, 3D, 4D, ...). It assumes all points are one dimensional numpy arrays (or two dimensional with one dimension shape 1). I am not sure if you require the projection to fall onto line segment or the extension of segment so I include both. You can pick whichever fits your question the best:
#distance between p1 and p2
l2 = np.sum((p1-p2)**2)
if l2 == 0:
print('p1 and p2 are the same points')
#The line extending the segment is parameterized as p1 + t (p2 - p1).
#The projection falls where t = [(p3-p1) . (p2-p1)] / |p2-p1|^2
#if you need the point to project on line extention connecting p1 and p2
t = np.sum((p3 - p1) * (p2 - p1)) / l2
#if you need to ignore if p3 does not project onto line segment
if t > 1 or t < 0:
print('p3 does not project onto p1-p2 line segment')
#if you need the point to project on line segment between p1 and p2 or closest point of the line segment
t = max(0, min(1, np.sum((p3 - p1) * (p2 - p1)) / l2))
projection = p1 + t * (p2 - p1)
Numpy code that works for both 2D and 3D (based on https://gamedev.stackexchange.com/questions/72528/how-can-i-project-a-3d-point-onto-a-3d-line):
import numpy as np
def point_on_line(a, b, p):
ap = p - a
ab = b - a
result = a + np.dot(ap, ab) / np.dot(ab, ab) * ab
return result
A = np.array([2, 0])
B = np.array([4, 4])
P = np.array([1, 3])
projected = point_on_line(A, B, P)
print(projected)
Update
Plot:
A = np.array([ 10.5, 15.6 ])
B = np.array([ 2, 6 ])
P = np.array([ 18.561, -19.451])
projected = point_on_line(A, B, P)
print(projected)
# [-3.35411076 -0.04699568]
plt.xlim(-20, 20)
plt.ylim(-20, 20)
plt.axis('equal')
x_values = [A[0], B[0]]
y_values = [A[1], B[1]]
plt.plot(B[0], B[1], 'ro')
plt.plot(A[0], A[1], 'ro')
plt.plot(P[0], P[1], 'ro')
plt.plot(x_values, y_values, 'b-')
plt.plot(projected[0], projected[1], 'rx')
Update 2
If you need the point to belong to the segment, you need to make a small amendment
def point_on_line(a, b, p):
ap = p - a
ab = b - a
t = np.dot(ap, ab) / np.dot(ab, ab)
# if you need the the closest point belonging to the segment
t = max(0, min(1, t))
result = a + t * ab
return result