I am going to implement binary addition by Recurrent Neural Network (RNN) as a sample. I have coped with an issue to implement it by Python, so I decided to share my problem in there to come up with ideas to fix it.
As can be seen in my notebook code (Backpropagation through time (BPTT) section), There is a chain rule like below to update input weight matrix like below:
My problem is this part:
I've tried to implement this part in my Python code or notebook code (class input_layer, backward method), but unmatched dimensions raises an error.
In my sample code, W_hidden is 16*16, whereas the result of delta pre_hidden is 1*2. This makes the error. If you run the code, you could see the error.
I spent a lot of time to check my chain rule as well as my code. I guess my chain rule is right. Only reason to make this error is my code.
As I know, multiple unmatched matrices in terms of dimension is impossible. If my chain rule is correct, how it could be implemented by Python? Any idea?
Thanks in advance.

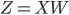 , and
, and 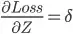 , we will have:
, we will have: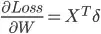 ,
, 