Robustly finding the local maximum of an image patch with sub-pixel accuracy

Question

I am developing a SLAM algorithm in C, and I have implemented the FAST corner finding method which gives me some strong keypoints in the image. The next step is to get the center of the keypoints with a sub-pixel accuracy, therefore I extract a 3x3 patch around each of them, and do a Least Squares fit of a two dimensional quadratic:

quad

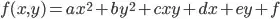
Where f(x,y) is the corner saliency measure of each pixel, similar to the FAST score proposed on the original paper, but modified to also provide a saliency measure in non corner pixels.

And the least squares:

bhat

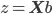
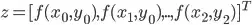
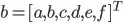
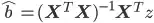
With 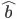being the estimated parameters.
I can now calculate the location of the peak of the fitted quadratic, by taking the gradient equal to zero, achieving my original goal.

The issue arises on some corner cases, where the local peak is closer to the edge of the window, resulting in a fit with low residuals but a peak of the quadratic way outside the window.

An example:
The corner saliency and a contour of the fitted quadratic:

The saliency (blue) and fit (red) as 3D meshes:

Numeric values of this example are (row-major ordering):

[336, 522, 483, 423, 539, 153, 221, 412, 234]

And the resulting sub pixel center of (2.6, -17.1) being wrong.

How can I constrain the fit so the center is within the window?
I'm open to alternative methods for finding the sub pixel peak.

Hi @YvesDaoust , thanks for your reply. I have tested the fit with synthetic data and it seems to perform as expected. Any other ideas maybe? — Bobisnotyouruncle, Apr 15 '20 at 17:16
Is the fit wrong because your inverse matrix is unstable? Did you try solving the equation using a singular value decomposition? — Cris Luengo, Apr 15 '20 at 18:50
@YvesDaoust The values are [336, 522, 483, 423, 539, 153, 221, 412, 234] (Row major but I guess that's irrelevant). — Bobisnotyouruncle, Apr 15 '20 at 19:06
@CrisLuengo I did not try with SVD because I originally was confident about the fit, but I tried with Moore-Penrose pseudoinverse with same results. I am not sure that this verifies that though — Bobisnotyouruncle, Apr 15 '20 at 19:07

score 3 · Answer 1 · answered Apr 15 '20 at 18:37

3

The obvious answer is to reject 3x3 (or 5x5, whatever you use) boxes whose discrete maximum is not at the center. In other words, to use a quadratic approximation only to refine the location of a maximum that must be located inside the box.

More generally, in such cases the first questions to ask is not "How do I constrain my model-fitting procedure to shoehorn a solution for this edge case?", but rather "Does my model apply to this edge case?" and "Is this edge case even worth spending time on, or can I just ignore it?"

answered Apr 15 '20 at 18:37

Francesco Callari

11,300
2
25
40

I see your point, but I believe that I should develop a solution which handles cases like these, since the local maxima is in the 3x3 region. A solution for example which also has as a cost the distance of (x0,y0) from (1,1) came to my mind, but unfortunately I cannot afford (computationally wise) optimization algorithms. There must be a trick that is eluding me.. Thank you for your answer – Bobisnotyouruncle Apr 15 '20 at 19:10

score 2 · Accepted Answer · answered Apr 15 '20 at 19:26

2

I tried my own code to fit a 2D quadratic function to the 3x3 values, using a stable least-squares solving algorithm, and also found a maximum outside of the domain. The 3x3 patch of data does not match a quadratic function, and therefore the fit is not useful.

Fitting a 2D quadratic to a 3x3 neighborhood requires a degree of smoothness in the data that you don't seem to have in your FAST output.

There are many other methods to find the sub-pixel location of the maximum. One that I like because it is more stable and less computationally intensive is the fitting of a "separable" quadratic function. In short, you fit a quadratic function to the three values around the local maximum in one dimension, and then another in the other dimension. Instead of solving 6 parameters with 9 values, this solves 3 parameters with 3 values, twice. The solution is guaranteed stable, as long as the center pixel is larger or equal to all pixels in the 4-connected neighborhood.

z1 = [f(-1,0), f(0,0), f(1,0)]^T

    [1,-1,0]
X = [0,0,0]
    [1,1,0]

solve: X b1 = z1

and

z2 = [f(0,-1), f(0,0), f(0,1)]^T

    [1,-1,0]
X = [0,0,0]
    [1,1,0]

solve: X b2 = z2

Now you get the x-coordinate of the centroid from b1 and the y-coordinate from b2.

answered Apr 15 '20 at 19:26

Cris Luengo

55,762
10
62
120

That's certainly a good idea. That way though discards the information present on the four unused pixels of the window, and I am not sure what would be the effects of that. Would repeating this process for the diagonals and getting the center as the mean of the two points be better in your opinion? Thanks – Bobisnotyouruncle Apr 15 '20 at 19:53
@Bobisnotyouruncle: You could certainly try that. Do remember that, for the diagonals, the distances between pixels are `sqrt(2)`, not `1`. And because those distances are larger, you might want to think about a weighted average where the result from the diagonals weigh a bit less than the result from the main axes. – Cris Luengo Apr 15 '20 at 20:01
@Bobisnotyouruncle: Though if sub-pixel precision is important, you might want to consider a corner detector that produces a smooth output. FAST uses all sorts of ugly filtering kernels that cause the non-smooth output. Using proper Gaussian filtering for the derivatives leads to a smooth output where interpolation actually makes sense, and where every 3x3 patch can be properly modelled by a 2D quadratic. – Cris Luengo Apr 15 '20 at 20:04
Thanks, I'll try that. The reason for using FAST is extreme computational power limitations, and my thinking was that the sub pixel method should be based on the FAST saliency score, since this is the measure which will be higher for the center pixel of the neighborhood – Bobisnotyouruncle Apr 15 '20 at 20:21

Robustly finding the local maximum of an image patch with sub-pixel accuracy

2 Answers2