Using Python and SymPy I am trying to solve this equation for b:
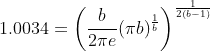
My code:
From sympy import *
b = Symbol('b')
x = ((b/(2*math.pi*math.e))*((math.pi*b)**(1/b)))**(1/(2*(b-1)))
solve(x-1.0034,b)
And I get this error: NotImplementedError: multiple generators...No algorithms are implemented to solve equation...
Do you know where is the mistake? Or is it possible that the equaiton is so difficult that Python can not solve it? Thank you
It's better to use pi and E from sympy:
In [21]: b = Symbol('b')
In [22]: eq = ((b/(2*math.pi*math.e))*((math.pi*b)**(1/b)))**(1/(2*(b-1))) - 1.0034
In [23]: eq
Out[23]:
1
───────
2⋅b - 2
⎛ b ____________________⎞
⎝0.0585498315243192⋅b⋅╲╱ 3.14159265358979⋅b ⎠ - 1.0034
In [24]: eq = ((b/(2*pi*E))*((pi*b)**(1/b)))**(1/(2*(b-1))) - 1.0034
In [25]: eq
Out[25]:
1
───────
2⋅b - 2
⎛ b _____ -1⎞
⎜b⋅╲╱ π⋅b ⋅ℯ ⎟
⎜─────────────⎟ - 1.0034
⎝ 2⋅π ⎠
The equation is transcendental and it is unlikely that analytic solutions exist. Potentially there is a Lambert form for this but solve does not find anything.
You can solve it numerically though using nsolve:
In [29]: sol = nsolve(eq, b, 2)
In [30]: sol
Out[30]: 14.3368885826882
In [31]: eq.n(subs={b:sol})
Out[31]: 7.22915270916583e-19
