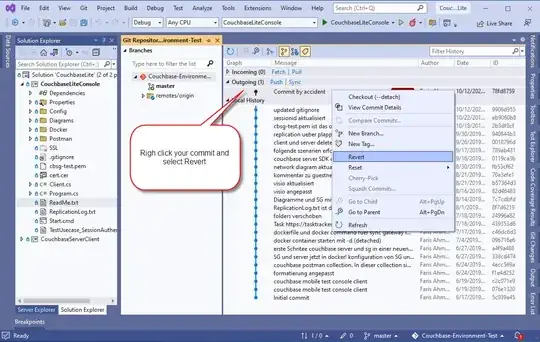
I am not so good in math and I have an interview question to answer but I can`t understand this equation: the interview question is: write a function that, given an integer N(1 <= N <= 100) returns array containing N unique integer that sum up to 0.
I cant understand it to solve it please help what N(1 <= N <= 100) this mean.
P.S: I am not looking for ready solution, I want understand the concept so I can solve it my self. Thanks.
Edit: its not a range from 1,100 as you`re suggesting, here is the question image