What is the algebra that allows this optimization for prime finding?

Question

I missed this optimization in an interview and wanted to review the algebra that allows it:

for(let j = 2; j * j < i; j++){

The line above in the code below, were instead of using j < i, we use j * j < i or equivalently, .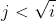

Is this basic algebra we learned in grade school that I forgot? Can a reference be provided to an algebra cheat sheet or similar?

// prime-2
// 2 optimizations - odds and square root
function prime2(n){
  const primes = [2];

  // first optimization is to only check odd numbers ...
  not_prime: for(let i = 3; i < n; i += 2){

    // second optimization is to only check up to ...
    // the square root of j when looking for factors
    for(let j = 2; j * j < i; j++){
      if(i % j === 0){
        continue not_prime;
      }
    }
    primes.push(i);
  }
  return primes;
}

Answer 1

LeetCode has this as a problem (Count Primes) and has a helpful hint to help you understand this:

Let's write down all of 12's factors:

2 × 6 = 12

3 × 4 = 12

4 × 3 = 12

6 × 2 = 12

As you can see, calculations of 4 × 3 and 6 × 2 are not necessary. Therefore, we only need to consider factors up to √n because, if n is divisible by some number p, then n = p × q and since p ≤ q, we could derive that p ≤ √n.

Answer 2

I think it should be j * j <= i. The reasoning is that if i is not a prime then you have i == p*q where p is a prime smaller-or-equal q i.e. p<=q. So for example in the worst case 49 is 7*7. You don't need to check beyond p e.g. 7+ because you already checked for the smaller prime.