Python curve fitting problem with peaked and flat-top (super) gaussian signals

Question

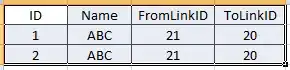
I have a standard gaussian function, that looks like this:

def gauss_fnc(x, amp, cen, sigma):
    return amp * np.exp(-(x - cen) ** 2 / (2 * sigma ** 2))

And I have a fit_gaussian function that uses scipy's curve_fit to fit my gauss_fnc:

from scipy.optimize import curve_fit

def fit_gaussian(x, y):
    mean = sum(x * y) / sum(y)
    sigma = np.sqrt(sum(y * (x - mean) ** 2) / sum(y))
    opt, cov = curve_fit(gauss_fnc, x, y, p0=[max(y), mean, sigma])
    values = gauss_fnc(x, *opt)
    return values, sigma, opt, cov

I can confirm that this works great if the data resembles a normal gaussian function, see example:

However if the signal is too peaked or too narrow, it won't work as expected. Example of a peaked gaussian:

Here is an example of a flat-top or super gaussian:

Currently the flatter the gaussian becomes, more and more information is lost, due to gaussian cutting down the edges. How can I improve the functions, or the curve fitting in order to be able to fit peaked and flat-top signals as well like in this picture:

Edit:

I provided a minimal working example to try this out:

from PyQt5.QtWidgets import (QApplication, QMainWindow)
from matplotlib.backends.backend_qt5agg import FigureCanvasQTAgg as FigureCanvas
from matplotlib.figure import Figure
from scipy.optimize import curve_fit
import numpy as np
from PyQt5.QtWidgets import QWidget, QGridLayout


def gauss_fnc(x, amp, cen, sigma):
    return amp * np.exp(-(x - cen) ** 2 / (2 * sigma ** 2))

def fit_gauss(x, y):
    mean = sum(x * y) / sum(y)
    sigma = np.sqrt(sum(y * (x - mean) ** 2) / sum(y))
    opt, cov = curve_fit(gauss_fnc, x, y, p0=[max(y), mean, sigma])
    vals = gauss_fnc(x, *opt)
    return vals, sigma, opt, cov


class MainWindow(QMainWindow):
    def __init__(self):
        super().__init__()
        self.results = list()

        self.setWindowTitle('Gauss fitting')
        self.setGeometry(50, 50, 1280, 1024)
        self.setupLayout()

        self.raw_data1 = np.array([1, 1, 1, 1, 3, 5, 7, 8, 9, 10, 11, 10, 9, 8, 7, 5, 3, 1, 1, 1, 1], dtype=int)
        self.raw_data2 = np.array([1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 200, 2, 1, 1, 1, 1, 1, 1, 1, 1, 1], dtype=int)
        self.raw_data3 = np.array([1, 1, 1, 1, 1, 3, 5, 9, 10, 10, 10, 10, 10, 9, 5, 3, 1, 1, 1, 1, 1], dtype=int)

        self.plot()

    def setupLayout(self):
        # Create figures
        self.fig1 = FigureCanvas(Figure(figsize=(5, 4), dpi=100))
        self.fig1AX = self.fig1.figure.add_subplot(111, frameon=False)
        self.fig1AX.get_xaxis().set_visible(True)
        self.fig1AX.get_yaxis().set_visible(True)
        self.fig1AX.yaxis.tick_right()
        self.fig1AX.yaxis.set_label_position("right")

        self.fig2 = FigureCanvas(Figure(figsize=(5, 4), dpi=100))
        self.fig2AX = self.fig2.figure.add_subplot(111, frameon=False)
        self.fig2AX.get_xaxis().set_visible(True)
        self.fig2AX.get_yaxis().set_visible(True)
        self.fig2AX.yaxis.tick_right()
        self.fig2AX.yaxis.set_label_position("right")

        self.fig3 = FigureCanvas(Figure(figsize=(5, 4), dpi=100))
        self.fig3AX = self.fig3.figure.add_subplot(111, frameon=False)
        self.fig3AX.get_xaxis().set_visible(True)
        self.fig3AX.get_yaxis().set_visible(True)
        self.fig3AX.yaxis.tick_right()
        self.fig3AX.yaxis.set_label_position("right")

        self.widget = QWidget(self)
        grid = QGridLayout()
        grid.addWidget(self.fig1, 0, 0, 1, 1)
        grid.addWidget(self.fig2, 1, 0, 1, 1)
        grid.addWidget(self.fig3, 2, 0, 1, 1)
        self.widget.setLayout(grid)
        self.setCentralWidget(self.widget)

    def plot(self):
        x = len(self.raw_data1)

        xvals, sigma, optw, covar = fit_gauss(range(x), self.raw_data1)
        self.fig1AX.clear()
        self.fig1AX.plot(range(len(self.raw_data1)), self.raw_data1, 'k-')
        self.fig1AX.plot(range(len(self.raw_data1)), xvals, 'b-', linewidth=2)
        self.fig1AX.margins(0, 0)
        self.fig1.figure.tight_layout()
        self.fig1.draw()

        xvals, sigma, optw, covar = fit_gauss(range(x), self.raw_data1)
        self.fig2AX.clear()
        self.fig2AX.plot(range(len(self.raw_data2)), self.raw_data2, 'k-')
        self.fig2AX.plot(range(len(self.raw_data2)), xvals, 'b-', linewidth=2)
        self.fig2AX.margins(0, 0)
        self.fig2.figure.tight_layout()
        self.fig2.draw()

        self.fig3AX.clear()
        self.fig3AX.plot(range(len(self.raw_data3)), self.raw_data3, 'k-')
        self.fig3AX.plot(range(len(self.raw_data3)), xvals, 'b-', linewidth=2)
        self.fig3AX.margins(0, 0)
        self.fig3.figure.tight_layout()
        self.fig3.draw()

if __name__ == '__main__':
    app = QApplication([])
    window = MainWindow()
    window.show()
    app.exec_()

Last picture is from here.

Do you want to modify your fitted function or are you after a different fitting method that fits your original gaussian? These are two very different approaches. — Gabriel, Feb 22 '20 at 14:48
If it's possible, I would like the original function to be modified in order to be universal. If it is not possible, a separate function for peaked gauissian and separate function for super gaussian is fine too. — kalzso, Feb 22 '20 at 14:54
Then it looks like you are after the [Generalized normal distribution](https://en.wikipedia.org/wiki/Generalized_normal_distribution). There's an implementation in scipy: [`scipy.stats.gennorm`](https://docs.scipy.org/doc/scipy-0.16.0/reference/generated/scipy.stats.gennorm.html) — Gabriel, Feb 23 '20 at 13:19
Thanks I will look into it. Or if you implement it into my minimal working example, and post it as answer, I could give you the bounty! — kalzso, Feb 24 '20 at 08:27

Zaraki Kenpachi · Accepted Answer · 2020-02-27T14:00:06.807

1

You can use Gaussian defined function for curve fit:

import numpy as np
from matplotlib import pyplot as plt
from scipy.optimize import curve_fit

x = range(21)
y_peak = np.array([1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 200, 2, 1, 1, 1, 1, 1, 1, 1, 1, 1], dtype=int)
y_flat_top = np.array([1, 1, 1, 1, 1, 3, 5, 9, 10, 10, 10, 10, 10, 9, 5, 3, 1, 1, 1, 1, 1], dtype=int)


# define gauss function
def Gauss(x, a, x0, sigma):
    return a * np.exp(-(x - x0)**2 / (2 * sigma**2))


# fit function
popt, pcov = curve_fit(Gauss, x, y_peak)

# set data for curve plot
x_fit = np.linspace(0,21,1000)
y_fit = Gauss(x_fit, popt[0], popt[1], popt[2])
y_fit = Gauss(x_fit, max(y_flat_top) , popt[1], popt[2])

# plot data
fig, ax = plt.subplots()
plt.plot(x, y_peak, '.')
plt.plot(x_fit, y_fit, '-', label='peak')
plt.legend()
plt.show()

Output:

With usage of Generalized normal distribution: It is hard to fit. You can play with bounds and try to add some additional parameters to function to get better fit. Another option is to use differential evolution algorithm to find best fit.

import matplotlib.pyplot as plt
import numpy as np
from scipy.optimize import curve_fit


# set data
x = np.linspace(-4, 4, 20)
y_peak = np.array([1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 200, 2, 1, 1, 1, 1, 1, 1, 1, 1], dtype=int)
y_flat_top = np.array([1, 1, 1, 1, 1, 3, 5, 9, 10, 10, 10, 10, 10, 9, 5, 3, 1, 1, 1, 1], dtype=int)
y = y_peak

# define generalized normal distribution
def general_norm(x, gamma, beta):
    value = (beta/(2*gamma*(1/beta)))*np.exp(-np.abs(x)**beta)
    return value


# set bounds
bounds_peak = ((0,0),(100,9))
bounds_flat_top = ((0,7),(100,9))

# fit function
popt, pcov = curve_fit(general_norm, x, y, bounds=bounds_peak)

# calculate rms
rms = sum((y - general_norm(x, popt[0], popt[1]))**2)

# set data for curve plot
x_fit = np.linspace(-4,4,1000)
y_fit = general_norm(x_fit, popt[0], popt[1])

# plot data
fig, ax = plt.subplots(1, 1)
ax.plot(x, y, '.')
ax.plot(x_fit, y_fit, 'b-')
plt.show()

Output:

edited Feb 27 '20 at 14:00

answered Feb 27 '20 at 10:15

Zaraki Kenpachi

5,510
2
15
38

I appreciate your effort, but that is exactly what I did, have you read the question? The normal gaussian won't fit the signal correctly if it's too narrow, or if it's too flat-top. – kalzso Feb 27 '20 at 10:20
@kalzso then post you peak/flat data or generated peak/flat data for test. – Zaraki Kenpachi Feb 27 '20 at 10:22
I can't because that is extracted from a livestream camera image. As you can see from the post, I mark the signal's maximum point as well (with a red dot). If I fit a normal gaussian to a flat-top signal, the max of the gaussian will be higher than the max of the flat-top signal, that is bad. Also it will cut down the edges of the flat-top, so we lose information there. I need to fit a function that resembles the original signal the best way possible. – kalzso Feb 27 '20 at 10:32
@kalzso for flat you can define `a` parameter as `max(y_flat_top) `, see update – Zaraki Kenpachi Feb 27 '20 at 11:02
still cutting down the edges, information is lost there. I need a generalised solution that works for every type of gaussian not just for normal. See Gabriel's comment above, I think he is on the right track. – kalzso Feb 27 '20 at 12:06
Looks better! When the signal is too peaked your solution is not too good, but I will accept your answer! – kalzso Feb 27 '20 at 14:12
@kalzso you can try play with `differential evolution` do find lowest `rms` and best fit. – Zaraki Kenpachi Feb 27 '20 at 14:15
How do you calculate the bounds? – kalzso Apr 20 '20 at 14:59

Python curve fitting problem with peaked and flat-top (super) gaussian signals

1 Answers1