0

I have a function given by a list of points, ex:

f = [0.03, 0.05, 0.02, 1.3, 1.0, 5.6, ..., 13.4, 12.45]

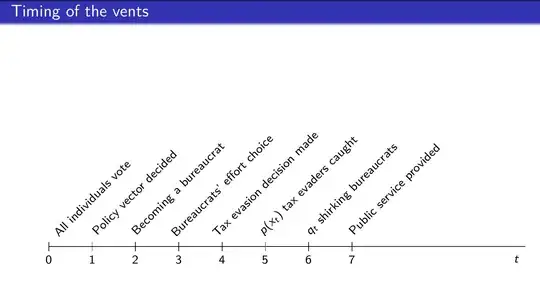
I need an algorithm (with linear complexity) to "cut" this function/list into K intervals/sublists so that each interval/sublist contains points that "lie near a line segment" (take a look at the image) enter image description here

The number K may be decided either by the algorithm itself or be a parameter of the algorithm. (preferable is to be decided by the algorithm itself)

Is there such a known algorithm I could use ?

1 Answers1

0

i am writing with smartphone so this is short. Basically a function is nearly linear if the difference between two consecutive values is approximately equal see http://psn.virtualnerd.com/viewtutorial/PreAlg_13_01_0006

As an algorithm for traversing an unsorted array Sliding Window is nice ( https://www.geeksforgeeks.org/window-sliding-technique/ ) and can be implemented by a single pass (1-pass solution)

Update because comment :

So with a sliding window you can implement the vagueness or fuzziness of the values you mentioned in the comment this is why nearly linear and approximately, i.e. 

if(abs(abs(x[i]-x[i+1]) - abs(x[i+1]-x[i+2])) < 0.5)
      {linearity_flag=1;} 
else 
      {linearity_flag=0;}

where x[i]-x[i+1] and x[i+1]-x[i+2] are two consecutive differences of two consecutive values and 0.5 is a deliberately chosen threshold that fixes what you define as a straight line or linear function in an x-y graph (or what 'jittering' of the line you allow). So you have to use the difference of differences of consecutive values. Instead of 3 points you can also include more points with this approach (sliding window)

If you want a strict mathematical ansatz you could use other curve analysis techniques : https://openstax.org/books/calculus-volume-1/pages/4-5-derivatives-and-the-shape-of-a-graph (actually the difference of differences of consecutive values is a discrete realization of a 2nd derivative)

ralf htp
  • 9,149
  • 4
  • 22
  • 34
  • The problem is that no three consecutive points lie on a line, so my K will be equal to N (the number of points). I need something more "fuzzier" to reduce the K. For example if I have N = 10000 points, I need K to be something like 100 or less. My funtion respresents prices of a stock per day, so it's not something weird like ```[100, -100, 250, 3, 75]```. So I need something like a heuristic algorithm to find intervals where the price has a "near" constant rate of change. –  Feb 08 '20 at 12:32