Jacobian determinant of vector-valued function with Python JAX/Autograd

Question

I have a function that maps vectors onto vectors

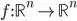
and I want to calculate its Jacobian determinant

,

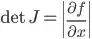where the Jacobian is defined as

.

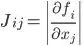Since I can use numpy.linalg.det, to compute the determinant, I just need the Jacobian matrix. I know about numdifftools.Jacobian, but this uses numerical differentiation and I'm after automatic differentiation. Enter Autograd/JAX (I'll stick to Autograd for now, it features an autograd.jacobian() method, but I'm happy to use JAX as long as I get what I want). How do I use this autograd.jacobian()-function correctly wit ha vector-valued function?

As a simple example, let's look at the function


which has the Jacobian


resulting in a Jacobian determinant

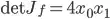
>>> import autograd.numpy as np
>>> import autograd as ag
>>> x = np.array([[3],[11]])
>>> result = 4*x[0]*x[1]
array([132])
>>> jac = ag.jacobian(f)(x)
array([[[[ 6],
         [ 0]]],


       [[[ 0],
         [22]]]])
>>> jac.shape
(2, 1, 2, 1)
>>> np.linalg.det(jac)
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
  File "/usr/lib/python3.8/site-packages/autograd/tracer.py", line 48, in f_wrapped
    return f_raw(*args, **kwargs)
  File "<__array_function__ internals>", line 5, in det
  File "/usr/lib/python3.8/site-packages/numpy/linalg/linalg.py", line 2113, in det
    _assert_stacked_square(a)
  File "/usr/lib/python3.8/site-packages/numpy/linalg/linalg.py", line 213, in _assert_stacked_square
    raise LinAlgError('Last 2 dimensions of the array must be square')
numpy.linalg.LinAlgError: Last 2 dimensions of the array must be square

A first approach gives me correct values, but the wrong shape. Why does .jacobian() return such a nested array? If I reshape it correctly, I get the correct result:

>>> jac = ag.jacobian(f)(x).reshape(-1,2,2)
array([[[ 6,  0],
        [ 0, 22]]])
>>> np.linalg.det(jac)
array([132.])

But now let's take a look at how this works out with array broadcasting, when I try to evaulate the Jacobian determinant for multiple values of x

>>> x = np.array([[3,5,7],[11,13,17]])
array([[ 3,  5,  7],
       [11, 13, 17]])
>>> result = 4*x[0]*x[1]
array([132, 260, 476])
>>> jac = ag.jacobian(f)(x)
array([[[[ 6,  0,  0],
         [ 0,  0,  0]],

        [[ 0, 10,  0],
         [ 0,  0,  0]],

        [[ 0,  0, 14],
         [ 0,  0,  0]]],


       [[[ 0,  0,  0],
         [22,  0,  0]],

        [[ 0,  0,  0],
         [ 0, 26,  0]],

        [[ 0,  0,  0],
         [ 0,  0, 34]]]])
>>> jac = ag.jacobian(f)(x).reshape(-1,2,2)
>>> jac
array([[[ 6,  0],
        [ 0,  0]],

       [[ 0,  0],
        [ 0, 10]],

       [[ 0,  0],
        [ 0,  0]],

       [[ 0,  0],
        [14,  0]],

       [[ 0,  0],
        [ 0,  0]],

       [[ 0, 22],
        [ 0,  0]],

       [[ 0,  0],
        [ 0,  0]],

       [[26,  0],
        [ 0,  0]],

       [[ 0,  0],
        [ 0, 34]]])
>>> jac.shape
(9,2,2)

Here obviously both shapes are wrong, correct (as in the Jacobian matrix I want) woule be

[[[ 6,  0],
  [ 0, 22]],
 [[10,  0],
  [ 0, 26]],
 [[14,  0],
  [ 0, 34]]]

with shape=(6,2,2)

How do I need to use autograd.jacobian (or jax.jacfwd/jax.jacrev) in order to make it handle multiple vector inputs correctly?

---

Note: Using an explicit loop and treating every point manually, I get the correct result. But is there a way to do it in place?

>>> dets = []
>>> for v in zip(*x):
>>>    v = np.array(v)
>>>    jac = ag.jacobian(f)(v)
>>>    print(jac, jac.shape, '\n')
>>>    det = np.linalg.det(jac)
>>>    dets.append(det)
 [[ 6.  0.]
 [ 0. 22.]] (2, 2)

 [[10.  0.]
 [ 0. 26.]] (2, 2)

 [[14.  0.]
 [ 0. 34.]] (2, 2)

>>> dets
 [131.99999999999997, 260.00000000000017, 475.9999999999998]

Answer 1

"How do I use this autograd.jacobian()-function correctly with a vector-valued function?"

You've written

x = np.array([[3],[11]])

There are two issues with this. The first is that this is a vector of vectors, while autograd is designed for vector to vector functions. The second is that autograd expects floating point numbers, rather than ints. If you try to differentiate with respect to ints, you'll get an error. You aren't seeing an error with a vector of vectors because autograd automatically converts your lists of ints to lists of floats.

TypeError: Can't differentiate w.r.t. type <class 'int'>

The following code should give you the determinant.

import autograd.numpy as np
import autograd as ag

def f(x):
    return np.array([x[0]**2,x[1]**2])

x = np.array([3.,11.])
jac = ag.jacobian(f)(x)
result = np.linalg.det(jac)
print(result)

"How do I need to use autograd.jacobian (or jax.jacfwd/jax.jacrev) in order to make it handle multiple vector inputs correctly?"

There is a way to do it in place, it is called jax.vmap. See the JAX docs. (https://jax.readthedocs.io/en/latest/jax.html#vectorization-vmap)

In this case, I could compute a vector of Jacobian determinants with the following code. Note that I can define the function f in exactly the same way as before, vmap does the work for us behind the scenes.

import jax.numpy as np
import jax

def f(x):
    return np.array([x[0]**2,x[1]**2])

x = np.array([[3.,11.],[5.,13.],[7.,17.]])

jac = jax.jacobian(f)
vmap_jac = jax.vmap(jac)
result = np.linalg.det(vmap_jac(x))
print(result)