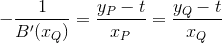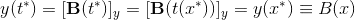Perpendicular line from bezier curve to point

Question

Question

I need to get the the point Q of a cubic (2d) bezier curve B(t) where the line from point Q to another given point P intersects perpendicular with the bezier curve.

• I know: P, B(t)
• I look for: Q (basically I want to have the slope of g but I can easily calculate this when I know Q, but the slope of g is enough)

---

What I did until now (you can skip this)

Note that I think this ansatz is wrong. This is only included for completeness.

I tried to solve this with my (basic) knowledge of mathematics but I cannot finish it. This is what I have now (please don't too strict with the notation, I'm not very good in this):

The following formulas will be expressed as y(x) to get one result this has to be calculated for y(x) and x(y). The point P is the control point, Q is the point where the line g(x) from Q to P is perpendicular on the bezier curve B(t) = (x, y)^T. The expression for the line g(x) can be retrieved by

where B(x) is the bezier curve in Cartesian coordinates, B'(x) the derivative (in Cartesian coordinates) and k is the intersection with the y axis. To get the slope of g(x) one has to solve

To calculate B(x) one has to solve B(t) for t and then plugging it back in B(t). So in each point on the bezier curve there is the relation

which also applies for the derivative B'(t).

The derivative of B(t) is (according to wikipedia)

Solving this for t (with wolfram alpha) results in

where a₀ = (P₁ - P₀)_x, a₁ = (P₂ - P₁)_x and a₂ = (P₃ - P₂)_x. Plugging the *t_i*s back in B(t) results in (wolfram alpha for t₁, wolfram alpha for t₂, wolfram alpha for t₃)

Now the next thing would be to use y = B'(x) and the second equation and eliminate x but I have no idea how and I don't even know if this is possible.

Answer 1

You already know derivative of Bezier curve - it describes tangent to the curve. This tangent should be perpendicular to QP vector. So you need to write both components of vector PQ and tangent vector T at this point

PQx = (1-t)^3 * P0.x + 3*t*(1-t)^2*P1.x  ... - P.x
PQy = (1-t)^3 * P0.y + ... - P.y
Tx = 3*(1-t)^2 * (P1.x - P0.x).... and so on
Ty = ....

and make equation for dot product of vectors T and QP (dot product is zero for perpendicular vectors):

 PQx * Tx + PQy * Ty = 0

Now open brackets and get equation of 5-th degree for unknown t.

There is no closed-form solution for such polynomial equation, so you need some kind of numerical root-finding algorithm (use those ones intended for polynomial roots)

Answer 2

I found a implementation for a approximation for my problem made by mbostock on Github who implemented the idea from this online book which was acutally created by @Mike'Pomax'Kamermans about bezier curves. If you have to deal with bezier curves check this out. This explains most of the problems I had with bezier curves.

The idea of the algorithm is the following one:

1. Make a rough approximation:
   1. Calculate Q_{approx, i} by plugging in different t_is in B(t) (mbostock uses t₁ = 0, t₂ = 1/8, t₃ = 2/8, ...).
   2. Calculate the quadratic (save one square root calculation) distance between Q_{approx, i} and P.
   3. Save the Q_{approx, i} and the t_i which is the closest (with the smallest distance).
2. Make a more precise approximation:
   1. Choose a precision q.
   2. Calculate t_before = t_i - q.
   3. Check if the distance between between Q_{approx, before} = B(t_before) and P is smaller than the distance between Q_{approx, i} and P, if yes set Q_{approx, i} = Q_{approx, before} and start at 2 (precise approximation), if no continue.
   4. Calculate t_after = t_i + q.
   5. Check if the distance between between Q_{approx, after} = B(t_after) and P is smaller than the distance between Q_{approx, i} and P, if yes set Q_{approx, i} = Q_after and start at 2 (precise approximation), if no continue.
   6. Q_{approx, i} is the closest. If the precision is good enough stop here. If not decrease the precision q (mbostock divides by two) and start over again at 2 (precise approximation).

As already mentioned there is the implementation of mbostock on Github. I paste the code here in case the link goes down. THIS IS NOT MY OWN CODE.

var points = [[474,276],[586,393],[378,388],[338,323],[341,138],[547,252],[589,148],[346,227],[365,108],[562,62]];
var width = 960,
    height = 500;
var line = d3.svg.line()
    .interpolate("cardinal");
var svg = d3.select("body").append("svg")
    .attr("width", width)
    .attr("height", height);
var path = svg.append("path")
    .datum(points)
    .attr("d", line);
var line = svg.append("line");
var circle = svg.append("circle")
    .attr("cx", -10)
    .attr("cy", -10)
    .attr("r", 3.5);
svg.append("rect")
    .attr("width", width)
    .attr("height", height)
    .on("mousemove", mousemoved);
// adding coordinates display
var coords = svg.append("text");
function mousemoved() {
  var m = d3.mouse(this),
      p = closestPoint(path.node(), m);
  line.attr("x1", p[0]).attr("y1", p[1]).attr("x2", m[0]).attr("y2", m[1]);
  circle.attr("cx", p[0]).attr("cy", p[1]);
  coords.attr("x", (p[0] + m[0]) / 2).attr("y", (p[1] + m[1]) / 2).html("Q(" + Math.round(p[0]) + ", " + Math.round(p[1]) + ")");
}
function closestPoint(pathNode, point) {
  var pathLength = pathNode.getTotalLength(),
      precision = 8,
      best,
      bestLength,
      bestDistance = Infinity;
  // linear scan for coarse approximation
  for (var scan, scanLength = 0, scanDistance; scanLength <= pathLength; scanLength += precision) {
    if ((scanDistance = distance2(scan = pathNode.getPointAtLength(scanLength))) < bestDistance) {
      best = scan, bestLength = scanLength, bestDistance = scanDistance;
    }
  }
  // binary search for precise estimate
  precision /= 2;
  while (precision > 0.5) {
    var before,
        after,
        beforeLength,
        afterLength,
        beforeDistance,
        afterDistance;
    if ((beforeLength = bestLength - precision) >= 0 && (beforeDistance = distance2(before = pathNode.getPointAtLength(beforeLength))) < bestDistance) {
      best = before, bestLength = beforeLength, bestDistance = beforeDistance;
    } else if ((afterLength = bestLength + precision) <= pathLength && (afterDistance = distance2(after = pathNode.getPointAtLength(afterLength))) < bestDistance) {
      best = after, bestLength = afterLength, bestDistance = afterDistance;
    } else {
      precision /= 2;
    }
  }
  best = [best.x, best.y];
  best.distance = Math.sqrt(bestDistance);
  return best;
  function distance2(p) {
    var dx = p.x - point[0],
        dy = p.y - point[1];
    return dx * dx + dy * dy;
  }
}

.disclaimer{
  padding: 10px;
  border-left: 3px solid #ffcc00;
  background: #fffddd;
}
path {
  fill: none;
  stroke: #000;
  stroke-width: 1.5px;
}
line {
  fill: none;
  stroke: red;
  stroke-width: 1.5px;
}
circle {
  fill: red;
}
rect {
  fill: none;
  cursor: crosshair;
  pointer-events: all;
}

<script src="https://cdnjs.cloudflare.com/ajax/libs/d3/3.5.17/d3.min.js"></script>
<div class="disclaimer">
  This is not my own code. This is made by <a href="https://gist.github.com/mbostock/8027637">mbostock on Github</a> based on Mike Kamermans <a href="https://pomax.github.io/bezierinfo/#projections">Primer on Bézier Curves online book</a>.
</div>