Regularized polynomial regression on linear data - penalize only degree 2 coefficient

Question

I've implemented gradient descent in Python to perform a regularized polynomial regression using as a loss function the MSE, but on linear data (to prove the role of the regularization).

So my model is under the form:

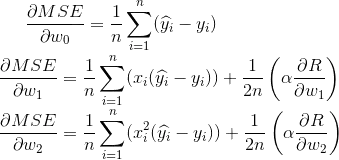
And in my loss function, R represents the regularization term:

Let's take the L2-norm as our regularization, the partial derivatives of the loss function w.r.t. wi are given below:

Finally, the coefficients wi are updated using a constant learning rate:

The problem is that I'm unable to make it converge, because the regularization is penalizing both of the coefficients of degree 2 (w2) and degree 1 (w1) of the polynomial, while in my case I want it to penalize only the former since the data is linear.

Is it possible to achieve this, as both LassoCV and RidgeCV implemented in Scikit-learn are able to do it? Or is there a mistake in my equations given above?

I suspect that a constant learning rate (mu) could be problematic too, what's a simple formula to make it adaptive?

Answer 1

I ended up using Coordinate descent as described in this tutorial to which I added a regularization term (L1 or L2). After a relatively large number of iterations, w2 was almost zero (and therefore the predicted model was linear).