Why isn't my random walk simulation working correctly?

Question

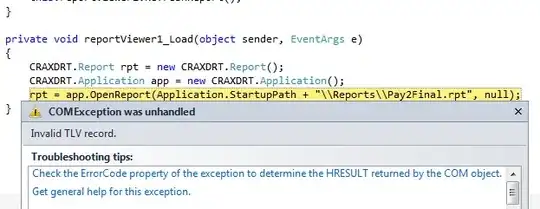
I have written the following code to simulate an unbiased random walk on Z^2. With probability 1/4, the "destination" is supposed to move one unit up, left, right, or down. So I made "destination" a matrix with two columns, one for the x-coordinate and one for the y-coordinate, and increment/decrement the appropriate coordinate as according to the value of runif(1).

N_trials <- 10
N_steps <- 10
destination <- matrix(0,N_trials,2)
for(n in 1:N_steps) {

    p <- runif(1)
    if(p < 1/4) {
      destination[n,1] <- destination[n,1] - 1
    }
    else if(p < 1/2) {
      destination[n,1] <- destination[n,1] + 1
    }
    else if(p < 3/4) {
      destination[n,2] <- destination[n,2] + 1
    }
    else if(p < 1) {
      destination[n,2] <- destination[n,2] - 1
    }
  }

However, the process never seems to move out of the set {(0,0),(1,0),(-1,0),(0,1),(0,-1)}. Why is this? Is there an error in the logic of my code?

Shouldn't it be more like `destination[n+1,1] <- destination[n,1] - 1`? Each row should depend on previous rows, no? — John Coleman, Dec 23 '19 at 03:23
Unfortunately making that change now has my code staying at (0,0) the whole time, giving me an error ```Error in destination[n + 1, 1] <- destination[n, 1] - 1 : replacement has length zero```. — Math1000, Dec 23 '19 at 03:26
I fixed that bug by changing ```for(i in 1:N_steps-1)``` to ```for(i in 1:(N_steps-1))```. But it still doesn't seem to be giving me the expected results... — Math1000, Dec 23 '19 at 03:47
Are you giving values to *both* `destination[n+1,1]` and `destination[n+1,2]` in all branches at each step? For example, `destination[n+1,1] <- destination[n,1] - 1` should be done in conjunction with `destination[n+1,2] <- destination[n,2]` — John Coleman, Dec 23 '19 at 03:57
that was my understanding (as @John pointed out) - currently you change either `x` or `y` and update either one, but you probably want to carry over the previous value on the dimension you didn't update... — Ben, Dec 23 '19 at 03:59
(Is this meant for large amounts of randomness? If so, it might be better to do a single call to `runif` and index it with `n`.) — r2evans, Dec 23 '19 at 04:49
No, the transition probabilities of moving to adjacent elements of Z^2 must be computed each time a move is made, so it is necessary to generate a U(0,1) random variable each such time. — Math1000, Dec 23 '19 at 04:51

score 3 · Answer 1 · answered Dec 23 '19 at 04:04

Here's what I have --- is this what you had in mind?

set.seed(1)

N_trials <- 10
N_steps <- 10
destination <- matrix(0, N_trials, 2)

for(n in 1:(N_steps-1)) {
  p <- runif(1)
  if(p < 1/4) {
    destination[n+1,1] <- destination[n,1] - 1
    destination[n+1,2] <- destination[n,2]
  }
  else if(p < 1/2) {
    destination[n+1,1] <- destination[n,1] + 1
    destination[n+1,2] <- destination[n,2]
  }
  else if(p < 3/4) {
    destination[n+1,1] <- destination[n,1]
    destination[n+1,2] <- destination[n,2] + 1
  }
  else if(p < 1) {
    destination[n+1,1] <- destination[n,1]
    destination[n+1,2] <- destination[n,2] - 1
  }
}

destination

      [,1] [,2]
 [1,]    0    0
 [2,]    1    0
 [3,]    2    0
 [4,]    2    1
 [5,]    2    0
 [6,]    1    0
 [7,]    1   -1
 [8,]    1   -2
 [9,]    1   -1
[10,]    1    0

Ah, of course! I wasn't copying the previous value from the coordinate that didn't change. No wonder the output was weird. Thanks for pointing it out. — Math1000, Dec 23 '19 at 04:29

score 3 · Accepted Answer · answered Dec 23 '19 at 13:08

Rather than using loops, you can vectorize the random walk.

The idea is to first create a matrix of possible steps:

steps <- matrix(c(0,0,-1,1,-1,1,0,0),nrow = 4)

which is:

     [,1] [,2]
[1,]    0   -1
[2,]    0    1
[3,]   -1    0
[4,]    1    0

Then you can feed random subscripts into it:

steps[sample(1:4,10,replace = TRUE),]

for example will create a matrix of 9 rows where each row is randomly chosen from the steps matrix.

If you rbind this with c(0,0) as a starting position, and then take the cumulative sum (cumsum) of each column, you have your walk. You can wrap this all in a function:

rand.walk <- function(n){
  steps <- matrix(c(0,0,-1,1,-1,1,0,0),nrow = 4)
  walk <- steps[sample(1:4,n,replace = TRUE),]
  walk <-rbind(c(0,0),walk)
  apply(walk,2,cumsum)
}

For example, plot(rand.walk(1000),type = 'l') produces a graph which looks something like:

Certainly your code is more elegant than mine. I've never been very good at "vectorizing" code. — Math1000, Dec 23 '19 at 20:38

Why isn't my random walk simulation working correctly?

2 Answers2