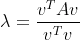0

I have a symmetric 3*3 matrix, A:

A = np.mat("1, 2, 1; 2, 5, 0; 1, 0, 5")

I have calculated the eigenvalues of A, which is 0, 6 and 5. I have now been told that A has the following three eigenvectors, and I am asked to find the corresponding three eigenvalues. How do I do this in Python?

   v1=np.array([[-5],[2], [1]])
   v2=np.array([[0],[-1], [2]])
   v3=np.array([[1],[2], [1]])

Afterwards I have to show that the three eigenvectors are linearly independent, which I also don't know how to show in Python?

user12541161
  • 21
  • 4

2 Answers2

2

To find the eigenvalue of a given eigenvector there is a well known formula (Rayleigh quotient):

eigenvalue

And to find if the eigenvectors are linearly independent, you can show that their determinant is different than zero:

import numpy as np

A = np.array([[1, 2, 1], [2, 5, 0], [1, 0, 5]])

v1 = np.array([[-5], [2], [1]])
v2 = np.array([[0], [-1], [2]])
v3 = np.array([[1], [2], [1]])

# eigenvalues
l1 = (v1.T@A@v1/(v1.T@v1))[0, 0]
l2 = (v2.T@A@v2/(v2.T@v2))[0, 0]
l3 = (v3.T@A@v3/(v3.T@v3))[0, 0]

# Are linearly independent?
tol = 1e-8
if np.abs(np.linalg.det(np.concatenate((v1, v2, v3), axis=1))) < tol:
    print('eigenvector are linearly dependent')
else:
    print('eigenvector are linearly independent')
Diego Palacios
  • 1,096
  • 6
  • 22
0

I am not sure what you have tried but here is the link that describes theoretical aspect on this topic.

In terms of python code, you can try this

import numpy as np
from numpy.linalg import eig
from numpy.linalg import det

A = np.mat("1, 2, 1; 2, 5, 0; 1, 0, 5")
values, vector = eig(A)
det(vector)
Pavan Kumar Polavarapu
  • 450
  • 3
  • 11
  • I have done that, and that worked - that gave me the det(A) which is 0, and the eigenvalues: 0, 6 and 5. However, my assignment now is to find the three eigenvalues corresponding to the three eigenvectors that I have been given (v1, v2, and v3 in my code) – user12541161 Dec 18 '19 at 14:36