I am training an autoencoder on data where each observation is a p=[p_1, p_2,...,p_n] where 0<p_i<1 for all i. Furthermore, each input p can be partitioned in parts where the sum of each part equals 1. This is because the elements represent parameters of a categorical distribution and p contains parameters for multiple categorical distributions.
As an example, the data that I have comes from a probabilistic database that may look like this:
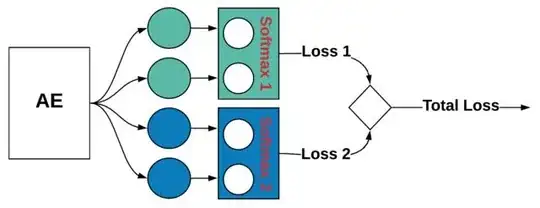
In order to enforce this constraint on my output, I use multiple softmax activations in the functional model API from Keras. In fact, what I am doing is similar to multi-label classification. This may look as follows:
The implementation is as follows:
encoding_dim = 3
numb_cat = len(structure)
inputs = Input(shape=(train_corr.shape[1],))
encoded = Dense(6, activation='linear')(inputs)
encoded = Dense(encoding_dim, activation='linear')(encoded)
decoded = Dense(6, activation='linear')(encoded)
decodes = [Dense(e, activation='softmax')(decoded) for e in structure]
losses = [jsd for j in range(numb_cat)] # JSD loss function
autoencoder = Model(inputs, decodes)
sgd = optimizers.SGD(lr=0.01, decay=1e-6, momentum=0.9, nesterov=True)
autoencoder.compile(optimizer=sgd, loss=losses, loss_weights=[1 for k in range(numb_cat)])
train_attr_corr = [train_corr[:, i:j] for i, j in zip(np.cumsum(structure_0[:-1]), np.cumsum(structure_0[1:]))]
test_attr_corr = [test_corr[:, i:j] for i, j in zip(np.cumsum(structure_0[:-1]), np.cumsum(structure_0[1:]))]
history = autoencoder.fit(train_corr, train_attr_corr, epochs=100, batch_size=2,
shuffle=True,
verbose=1, validation_data=(test_corr, test_attr_corr))
where structure is a list containing the number of categories that each attributes has, thus governing which nodes in the output layer are grouped and go to the same softmax layer. In the example above, structure = [2,2]. Furthermore, loss jsd is a symmetric version of the KL-divergence.
Question:
When using linear activation functions, the results are pretty good. However, when I try to use non-linear activation functions (relu or sigmoid), the results are much worse. What might be the reason for this?