0

I have to calculate a non-linear least-square regression for my ~30 data points following the formula

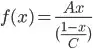
non-linear least-square formula

I tried the curve_fit function out of scipy.optimize using the following code

def func(x, p1 ,p2):
  return p1*x/(1-x/p2)

popt, pcov = curve_fit(func, CSV[:,1], CSV[:,0])

p1 = popt[0]
p2 = popt[1]

with p1 and p2 being equivalent to A and C, respectively, and CSV being my data-array. The functions runs without error message, but the outcome is not as expected. I've plotted the outcome of the function together with the original data points. I was not looking to get this nearly straight line (red line in plot), but something more close to the green line, which is simply a second order polynomial fit from Excel. The green dashed line shows just a quick manual try to get closer to the polynomial fit.

wrong calcualtin of the fit-function, together with the original data points: 1

Does anyone has an idea how to make the calculation run as i want it to?

Daemon Painter
  • 3,208
  • 3
  • 29
  • 44
Ueberkonsti
  • 5
  • 4
  • Your code is fine. There may be an suboptimal choice of formula vs dataset. Please share the data to run a test. – Poe Dator Dec 03 '19 at 17:17
  • Hope that works. I've saved the data as .csv file (easiest to work with in my oppinion) https://www.dropbox.com/s/54730mt5zaby18v/data.csv?dl=0 – Ueberkonsti Dec 03 '19 at 18:55

2 Answers2

0

Your code is fine. The data though is not easy to fit to. There are too few points on the right side of the chart and too much noise on the left hand side. This is why curve_fit fails. Some ways to improve the solution could be:

  • raising maxfev parameter for curve_fit() see here
  • giving starting values to curve_fit() - see same place
  • add more data points
  • use more parameters in the function or different function.

curve_fit() may not be the strongest tool. See if you can get better results with other regression-type tools.

Below is the best I could get with your initial data and formula:

df = pd.read_csv("c:\\temp\\data.csv", header=None, dtype = 'float' )
df.columns = ('x','y')

def func(x,  p1 ,p2):
    return p1*x/(1-x/p2)

popt, pcov = curve_fit(func, df.x, df.y,  maxfev=3000)
print('p1,p2:',popt)
p1, p2 = popt

y_pred = [ p1*x/(1-x/p2)+p3*x for x in range (0, 140, 5)]
plt.scatter(df.x, df.y)
plt.scatter(range (0, 140, 5), y_pred)

plt.show()

p1,p2: [-8.60771432e+02 1.08755430e-05]

enter image description here

Poe Dator
  • 4,535
  • 2
  • 14
  • 35
  • Ok, thanks. This helped me a lot. I am, however, not completely happy with the results, but to add a third parameter provided a nice correlation. One thing to add: the problems are not caused by the noise of the data. I've tried the code with the data points of the polynomial fit, and the result was similar. – Ueberkonsti Dec 04 '19 at 15:42
  • i think i've figured out a better way (see my answer above). – Ueberkonsti Dec 05 '19 at 09:41
0

I think i've figured out the best way to solve this problem by using the lmfit package (https://lmfit.github.io/lmfit-py/v). It worked best when i tried to fit the non-linear least-square regression not to the original data but to the fitting function provided by Excel (not very elegant, though).

from lmfit import Model
import matplotlib.pyplot as plt
import numpy as np

def func(x,  o1 ,o2):
    return o1*x/(1-x/o2) 

xt = np.arange(0, 0.12, 0.005)
yt = 2.2268*np.exp(40.755*xt)

model = Model(func)
result = model.fit(yt, x=xt, o1=210, o2=0.118)

print(result.fit_report())

plt.plot(xt, yt, 'bo')
plt.plot(xt, result.init_fit, 'k--', label='initial fit')
plt.plot(xt, result.best_fit, 'r-', label='best fit')
plt.legend(loc='best') 
plt.show

The results look pretty nice and the package is really easy to use (i've left out the final plot)

[[Fit Statistics]]
    # fitting method   = leastsq
    # function evals   = 25
    # data points      = 24
    # variables        = 2
    chi-square         = 862.285318
    reduced chi-square = 39.1947872
    Akaike info crit   = 89.9567771
    Bayesian info crit = 92.3128848
[[Variables]]
    o1:  310.243771 +/- 12.7126811 (4.10%) (init = 210)
    o2:  0.13403974 +/- 0.00120453 (0.90%) (init = 0.118)
[[Correlations]] (unreported correlations are < 0.100)
    C(o1, o2) =  0.930
Ueberkonsti
  • 5
  • 4