1

I'm new in asking at StackOverflow so sorry if using it in a wrong manner.

I have a maximize problem in a paper just like this:

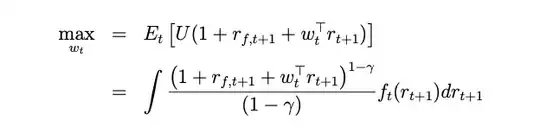
CRRA.png

and some constraints:

CodeCogsEqn.png

where r_f,t+1 and γ are given constant, r_t+1 is a multidimensional random variable vector(4 dimension here), f_t(r_t+1) is the multidimensional distribution function of the r_t+1. The problem is to find a weight vector w_t to maximize the expected value.

The paper said how it solves the problem, "The integrals are solved by simulating 100,000 variates for the 4 factors(the r_t+1 vector) from the multivariate conditional return distribution f_t(rt+1)". I know how to generate random numbers and get the mean from a distribution, but don't exactly know about how to use it in an optimization problem.

I have tried using some random numbers and return the mean value as the objective function, like the example below:

import numpy as np
rands = np.random.multivariate_normal(mean=[0, 0, 0, 0],
                                      cov=[[1, 0, 0, 0], [0, 1, 0, 0],
                                           [0, 0, 1, 0], [0, 0, 0, 1]],
                                      size=1000)


def expect_value(weight, rf, gamma, fac_ndarr):
    weight = np.asarray(weight)
    utility_array = (1 + rf + fac_ndarr.dot(weight))**(1 - gamma) / (1 - gamma)

    expected_value = utility_array.mean()
    return -expected_value

And the next, I use the module mystic to solve the global minimum.

from mystic.solvers import diffev2
from mystic.symbolic import (generate_conditions, generate_penalty,
                             generate_constraint, generate_solvers, simplify)

equation = """
x0 + x1 + x2 + x3 == 1
x0 + 2*(x1 + x2 + x3) - (1. / 0.2) <= 0
"""

pf = generate_penalty(generate_conditions(equation), k=1e20)
cf = generate_constraint(generate_solvers(simplify(equation)))
bounds = [(0, 1)] * 4

# Here the given constant `rf` and `gamma` are 0.15 and 7, 
# and they were passed to the parameter `args` with `rands`, 
# the `args` will be passed to the `cost`funtion.
result = diffev2(cost=expect_value,
                 args=(0.15, 7, rands),
                 x0=bounds,
                 bounds=bounds,
                 constraint=cf,
                 penalty=pf,
                 full_output=True,
                 npop=40)

My real problem generated 50000 random numbers, and it seems can't find the exact global minimum solution, since every time the code finds a different solution and the value of objective function differs. And even after reading the documentation and changing the parameter "npop" to 1000 and the "scale"(multiplier for mutations on the trial solution) to 0.1, it also didn't work as expected.

Is the way I used to solve the optimization problem wrong? What is the exact way to use simulation data in maximizing an expected value? Or there's something wrong in using the mystic module? Or, is there another efficient way to solve the maximization problem like above?

Thanks very much for your help！

C_Yue
  • 33
  • 6
  • If you give the values of the constants others can try it. You could also consider using scipy.minimize which allows for constraints (equality and equality, linear and nonlinear) – jeremy_rutman Dec 01 '19 at 07:28
  • @jeremy_rutman Thanks for your advice. The constants are in the `args` parameter of function `diffev2`, so the `rf` equals 0.15 and `gamma` equals 7 in this example. I will edit the post so it'll be obvious. I have tried scipy.minimize but it seems to work for the local minimum but not the global one. I've been trying scipy.optimize.basinhopping for global optimization in scipy but until now it doesn't succeed. – C_Yue Dec 01 '19 at 08:49
  • @jeremy_rutman: mystic is transparently breaking up the constraints into linear, nonlinear, equality, and inequality constraints. I don't think `scipy.minimize` is a good tool here. The OP wants an optimization of an expected value. `mystic` has modified versions of the `scipy` solvers that can provide this, while `scipy` cannot. – Mike McKerns Dec 02 '19 at 20:20
  • @C_Yue: my suggestion is to first add one of the verbose or logging `mystic.monitor` objects, so you can watch/plot the convergence of the solver. You may have a very nonlinear surface, and `diffev` needs to be tuned to solve for the global extrema... it can be difficult, depending on the surface. I'd also suggest trying one of the ensemble solvers to see if they do any better. You can also look the code in the `examples3` folder (on GitHub), and look into learning what the function surface looks like. For expected value calculations, look at `examples5`. – Mike McKerns Dec 02 '19 at 20:25

1 Answers1

0

mystic is built for this exact type of problem, as it can optimize in product measure space. See: https://github.com/uqfoundation/mystic/blob/master/examples5/TEST_OUQ_surrogate_diam.py

Mike McKerns
  • 33,715
  • 8
  • 119
  • 139