I have to create a PDA(pushdown automata) that accepts strings that not of the form 
.
For example it accepts 0011, 1100, 11000 but not accepts 1001, 011110, 0110.
How can I create this PDA? I know the answer of not accepting ww, but can't get an insight to make this one.
I would appreciate if you let me know the answer or nice hint to make it.
To accept ww^R, you push the symbols of w onto the stack, nondeterministically guess that you have reached the end of w, and then read w^R while popping matching symbols off the stack. The only way this can possibly accept is if your guess was right, and then it will only accept if your string is of the correct form.
To accept everything not of the form ww^R, consider the following:
First, nondeterministically guess about the parity of the input's length. If you guess that that the input has odd length, and you are right, then it is a string in the language since an odd-length string cannot be of the form ww^R. Doing this allows us to focus the other branch on the case of even-length strings not of the required form.
The defining characteristic of even-length strings not of the form ww^R is that for at least one index k from 1 to |w|, it is true that x[k] is not equal to x[2|w|-k+1]. So, we can push w onto the stack, just as a PDA for ww^R would; and we can nondeterministically guess that we have reached the end of w in the same way. However, instead of requiring the input symbols be equal to the top-of-stack symbols, we will pop a stack symbol for any input symbol, and we will further require that at least one of the input symbols does not match its corresponding top-of-stack symbol. We can do this by having two states for the popping phase: the first corresponding to not having encountered at least one mismatch, and the second corresponding to having seen one or more mismatches. Finally, we can accept if we are in the second of these states with no further input symbols and an empty stack.
Let ,
L = W W^R
The language L is a contest free language. So we can construct a push Down automata for L. There are generally two kinds of push down automata :
For the above language L Non-Deterministic push down automata is possible.
Here we can construct a PDA that accepts the language L and for the resultant PDA make all non-final states as final states and final state as non-final state.
PDA for W W^R is:
Initially Let q0 be the initial state and qf be the finial state.
∆(q0,0,Z0) = (q0, 0 Z0)
∆(q0,1,Z0) = (q0, 1 Z0)
∆(q0,0,1) = (q0, 01)
∆(q0,1,0) = (q0, 10)
∆(q0,0,0) = (q0, 00) or ∆(q0,0,0) = (q1, 00)
∆(q0,1,1) = (q0, 11) or ∆(q0,1,1) = (q1, 11)
∆(q1,0,0) = (q1,€)
∆(q1,b,b) = (q1,€)
∆(q1,€,Z0) = (qf,Z0)
where
∆ represents state transition.
€ represents pop operation.
The above is the Non-Deterministic PDA which accepts language W W^R. Now to construct a PDA which do not accept W W^R we need to make the initial state q0,q1 as final states and qf as non final state. And any string which does not reach qf is accepted by the PDA.
The PDA which accepts strings that are not of form W W^R is enclosed below:
In the above diagram q0,q1 are final states and qf is a non-final state. Any string which do not reach qf is accepted by PDA and if the string reaches PDA then the string must be rejected by PDA.
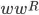