What would the equivalent Javascript equation be for this graph?

Question

I'm currently working on making an interface where I have image links that lean towards the mouse cursor. This is more for fun than as a serious project, but nevertheless the information I'm learning from it will be useful in the future. Right now I have several variables setup...

• diffx/y = the distance, in pixels, of the cursor from the link's original location. This value goes negative if the cursor goes to the left of or above the link's original location (already calculated).
• spacex/y = the amount of distance that I want in between the cursor and the link

• calcx/y = the calculated number will be added to the 'style.top' and 'style.left' of the link

  calcx = diffx - spacex
  calcy = diffy - spacey
  
  link.style.top = calcx
  link.style.top = calcy
  

If I set spacex/y = 0 the link is centered on the cursor
If I set spacex/y = diffx/y the link is set to its normal position

My goal is to have a link that leans slightly towards the cursor (maybe at max 40px from the original position) and
as the cursor gets closer to the link, the link will slowly return to its original position.
When the cursor gets within, let's say, 100px the link should (smoothly) jump towards the cursor as if to say "pick me!"

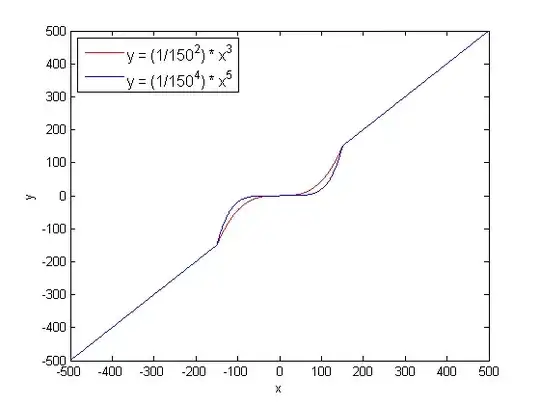
Here's what the equation would look like as a graph.

I need a way to write this as a javascript equation. I haven't taken algebra in awhile and I'm pretty sure we didn't go over anything that looked like this exactly. I'm guessing it has an exponent and a conditional in there somewhere, but I'm not quite sure. If your able to figure this out, I'd be really thankful (not to mention impressed).

Thank You for your help!

Answer 1

You'll definitely want a piecewise function here (the "conditional" you spoke of). The middle section appears to be an odd-powered polynomial of the form y = Ax^3 or y = Ax^5 for some small value of A (chosen to make y = 150 when x = 150). The curve appears to be essentially linear for |x| >= 200, that is y = x + B for x >= 200 and y = x - B for x <= -200. The transitions between 150 <= |x| <= 200 seem a little trickier, like a shifted exponential or quadratic. But you might start with this (pseudo code):

if (x < -150) {
    y = x;
} 
else if (x < 150) {
    y = (1.0/22500.0) * pow(x, 3);
}
else {  // x > 150
    y = x;
}

Note that this ignores the transitions between x = 150 and 200 and correspondingly assumes the constants B I mentioned above are zero. But it might get you started.

Edit:

After looking at a plot of my function, I think a 5th order polynomial matches your desired shape more closely. In this case, the middle function will be y = (1.0/506250000.0) * pow(x,5). Results are below. By the way, the constant values are equivalent to 150^-2 for the cubic, and 150^-4 for the quintic function.

Answer 2

I agree it is probably easier to model your function if you split it in parts:

f(x) = x + 50        if x < -200
       -150          if -200 <= x < -150
       150*(x/150)^k if -150 <= x < 150:
       150           if 150 <= x < 200
       x - 50        if 200 <= x

for k some big odd number (I'd try 4-10 out...)

Answer 3

You can use one or combination of these: http://drawlogic.com/2007/09/14/tweener-robert-penner-easing-equation-cheat-sheets/

Or http://www.robertpenner.com/easing/easing_demo.html