torch.softmax and torch.sigmoid are not equivalent in the binary case

Question

Given:

x_batch = torch.tensor([[-0.3, -0.7], [0.3, 0.7], [1.1, -0.7], [-1.1, 0.7]])

and then applying torch.sigmoid(x_batch):

tensor([[0.4256, 0.3318],
        [0.5744, 0.6682],
        [0.7503, 0.3318],
        [0.2497, 0.6682]])

gives a completely different result to torch.softmax(x_batch,dim=1):

tensor([[0.5987, 0.4013],
        [0.4013, 0.5987],
        [0.8581, 0.1419],
        [0.1419, 0.8581]])

As per my understanding, isn't the softmax is exactly the same as the sigmoid in the binary case?

score 7 · Answer 1 · edited May 06 '21 at 09:17

7

You are misinformed. Sigmoid and softmax are not equal, even for the 2 element case.

Consider x = [x1, x2].

sigmoid(x1) = 1 / (1 + exp(-x1))

but

softmax(x1) = exp(x1) / (exp(x1) + exp(x2))
            = 1 / (1 + exp(-x1)/exp(-x2))
            = 1 / (1 + exp(-(x1 - x2))
            = sigmoid(x1 - x2)

From the algebra we can see an equivalent relationship is

softmax(x, dim=1) = sigmoid(x - fliplr(x))

or in pytorch

x_softmax = torch.sigmoid(x_batch - torch.flip(x_batch, dims=(1,))

edited May 06 '21 at 09:17

iacob

20,084
6
92
119

answered Oct 24 '19 at 16:28

jodag

19,885
5
47
66

According to Bishop (Pattern recognition): `p(C1|x)=p(x|C_1)/(p(x|C1)*p(C1)+p(x|C2)*P(C2))` which is equal to `1/(1+exp(-a)` (sigmoid) In the multiclass problem is `p(Ck|x)=p(Ck|x)p(Ck)/` which is, for k=1 and j=2 the sigmoid – CutePoison Oct 25 '19 at 11:20
I don't understand what Bayes theorem has to do with this question, but I doubt Bishop claims that softmax of a vector is identical to applying the sigmoid function to each element of that vector. – jodag Oct 25 '19 at 14:42
I am not sure about Bishop, but even Andrew Ng mentions in his deeplearning.ai course that softmax reduces to sigmoid for binary classification. – akshayk07 Oct 27 '19 at 04:54
2

I showed in this answer that softmax is equivalent to sigmoid in a sense. Its equivalent to the sigmoid of the difference of logits, but not the sigmoid of the logits. – jodag Oct 27 '19 at 05:07

iacob · Answer 2 · 2021-08-28T17:29:23.417

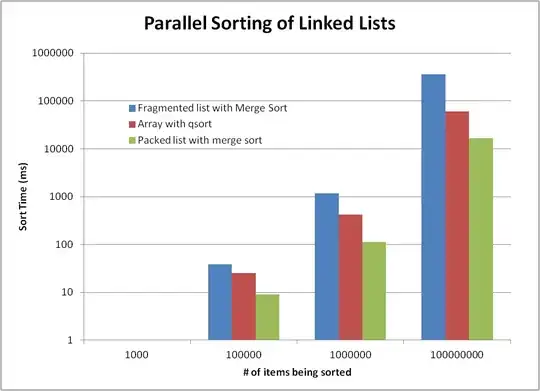
The sigmoid (i.e. logistic) function is scalar, but when described as equivalent to the binary case of the softmax it is interpreted as a 2d function whose arguments () have been pre-scaled by (and hence the first argument is always fixed at 0). The second binary output is calculated post-hoc by subtracting the logistic's output from 1.

Since the softmax function is translation invariant,¹ this does not affect the output:

The standard logistic function is the special case for a 1-dimensional axis in 2-dimensional space, say the x-axis in the (x, y) plane. One variable is fixed at 0 (say $z_{2}=0$ ), so , and the other variable can vary, denote it $z_{1}=x$ , so

${\textstyle e^{z_{1}}/\sum {k=1}^{2}e^{z{k}}=e^{x}/(e^{x}+1),}$ , the standard logistic function, and

${\textstyle e^{z_{2}}/\sum {k=1}^{2}e^{z{k}}=1/(e^{x}+1),}$ , its complement (meaning they add up to 1).

https://en.wikipedia.org/wiki/Softmax_function#Properties

Hence, if you wish to use PyTorch's scalar sigmoid as a 2d Softmax function you must manually scale the input (), and take the complement for the second output:

# Translate values relative to x0
x_batch_translated = x_batch - x_batch[:,0].unsqueeze(1)

###############################
# The following are equivalent
###############################

# Softmax
torch.softmax(x_batch, dim=1)

# Softmax with translated input
torch.softmax(x_batch_translated, dim=1)

# Sigmoid (and complement) with inputs scaled
torch.stack([1 - torch.sigmoid(x_batch_translated[:,1]), 
             torch.sigmoid(x_batch_translated[:,1])], dim=1)

tensor([[0.5987, 0.4013],
        [0.4013, 0.5987],
        [0.8581, 0.1419],
        [0.1419, 0.8581]])

tensor([[0.5987, 0.4013],
        [0.4013, 0.5987],
        [0.8581, 0.1419],
        [0.1419, 0.8581]])

tensor([[0.5987, 0.4013],
        [0.4013, 0.5987],
        [0.8581, 0.1419],
        [0.1419, 0.8581]])

^{More generally, softmax is invariant under translation by the same value in each coordinate: adding to the inputs yields , because it multiplies each exponent by the same factor, (because ), so the ratios do not change:

https://en.wikipedia.org/wiki/Softmax_function#Properties}

torch.softmax and torch.sigmoid are not equivalent in the binary case

2 Answers2