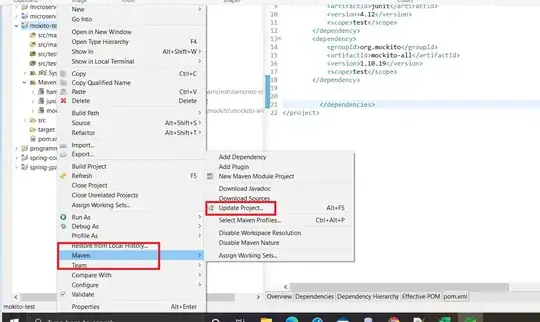
I have an oscillating data as shown in the below figure and want to fit a sine curve to it. However, my result is not correct.
The function that I want to fit to this curve is:
def radius (z,phi, a0, k0,):
Z = z.reshape(z.shape[0],1)
k = np.array([k0,])
a = np.array([a0,])
r0 = 110
rs = r0 + np.sum(a*np.sin(k*Z +phi), axis=1)
return rs
a correct solution could look like this:
r_fit = radius(z, phi=np.pi/.8, a0=10,k0=0.017)
plt.plot(z, r, label='data')
plt.plot(z, r_fit, label='fitted curve')
plt.legend()
My result however from fitting the curve looks:
from scipy.optimize import curve_fit
popt, pcov = curve_fit(radius, xdata=z, ydata=r)
r_fit = radius(z, *popt)
plt.plot(z, r, label='data')
plt.plot(z, r_fit, label='fitted curve')
plt.legend()
My data is also as follow:
r = np.array([100.09061214, 100.17932773, 100.45526772, 102.27891728,
113.12440802, 119.30644014, 119.86570527, 119.75184665,
117.12160143, 101.55081608, 100.07280857, 100.12880236,
100.39251753, 103.05404178, 117.15257288, 119.74048706,
119.86955437, 119.37452005, 112.83384329, 101.0507198 ,
100.05521567])
z = np.array([-407.90074345, -360.38004677, -312.99221012, -266.36934609,
-224.36240585, -188.55933945, -155.21242348, -122.02778866,
-87.84335638, -47.0274899 , 0. , 47.54559191,
94.97469981, 141.33801462, 181.59490575, 215.77219256,
248.95956379, 282.28027286, 318.16440024, 360.7246922 ,
407.940799 ])
since my function simply represents a Fourier series, I also tried scipy.fftpack.fft(r) but I couldn't reproduce a close signal to that of which I have calculated the fft.