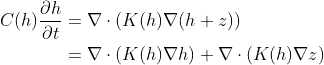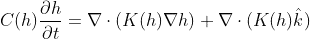C(h) \frac{\partial h}{\partial t}=\nabla \cdot(K(h) \nabla(h+z)) I have two questions:
- How do I represent a diffusive source that involve coordinate? The
governing equation is for h; k(h) is a function of h; z was the z
coordinate. I knew how to write a diffusive source without the
coordinate z, but I did not know how to represent a diffusive source
that involve coordinate.
- Do "phi[0].updateOld()"in the "...\fipy\examples\diffusion\mesh1D.py" update the "eq =transientTerm() == DiffusionTerm(coeff=D0 * (1 - phi[0]))" when just use "res = eq.sweep(var=phi[0], dt=timeStepDuration)"
Thanks for your help.