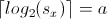I have two matricesFDX and TDX (two classes) with dim: 2xn, that FDX(1, :), FDX(2, :) are the number of objects and mean of them, respectively (also for TDX). I plot the above discrete sequence data using stem and now I want to show a curve instead of its lines to create a density map from points (like a pdf) or (like fit a curve to a Histogram), to better comparing between two classes.
Is there any way to fit a curve on the following plot of stem in Matlab?
I have also seen some links like link1 and also link2 but they are about histogram or continues data. Also, I have used the fit curve (link instead of the stem but two created curves are confusing.
Example:
FDX = [9,12,7,7,8,4,10,8,5,9,10; 0.626023067402372,0.647560923068733,0.266314729708634,0.512920709657816,0.408389652529404,0.444588941849425,0.800367166464757,1.28429713933315,0.391101796334982,0.219880153736852,0.439931802866314];
TDX = [1,1,2,1,1,1,1,1,1,1,1; 0.0888514059469934,0.0730468099283854,0.246560340244561,0.300711548987410,0.0871198693779434,3.11190476190476,0.185185185185183,0.246964650258985,0.113415750915749,0.132034632034618,0.201388888888900];
f1 = fit(TDX(2, :)', TDX(1, :)','smoothingspline');
plot(f1,'b', TDX(2, :)', TDX(1, :)','oc');
hold on
% stem(TDX(2, :), TDX(1, :),'*c');
grid on
hold on
f2 = fit(FDX(2, :)', FDX(1, :)','smoothingspline');
plot(f2,'r',FDX(2, :)', FDX(1, :)','om');
hold on
% stem(FDX(2, :), FDX(1, :),'*m');
grid on
hold off
title('Displacement Curve X', 'Units', 'normalized', 'Position', [2.5, 1.1, 0]);
xlabel('Mean')
ylabel('Number of Objs')
legend('MeanTDX','MeanFDX')
set(gcf, 'Units', 'Normalized', 'OuterPosition', [0 0 1 1]);
In the following, there are two plots of FDX and TDX with dimensions of 2x432 and 2x114, respectively.
and
Output of stem:
Output of fit:
A model that I want: