As a programmer how would you explain imaginary numbers?

Question

As a programmer I think it is my job to be good at math but I am having trouble getting my head round imaginary numbers. I have tried google and wikipedia with no luck so I am hoping a programmer can explain in to me, give me an example of a number squared that is <= 0, some example usage etc...

Answer 1

I guess this blog entry is one good explanation:

The key word is rotation (as opposed to direction for negative numbers, which are as stranger as imaginary number when you think of them: less than nothing ?)

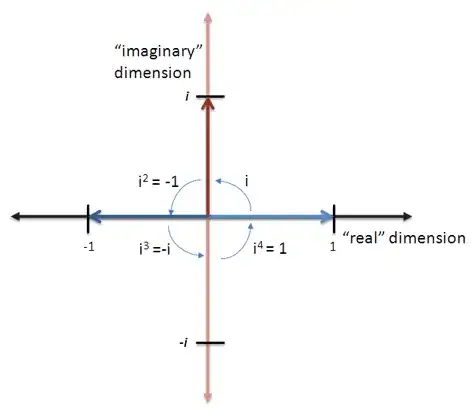
Like negative numbers modeling flipping, imaginary numbers can model anything that rotates between two dimensions “X” and “Y”. Or anything with a cyclic, circular relationship

Answer 2

Problem: not only am I a programmer, I am a mathematician. Solution: plow ahead anyway.

There's nothing really magical to complex numbers. The idea behind their inception is that there's something wrong with real numbers. If you've got an equation x^2 + 4, this is never zero, whereas x^2 - 2 is zero twice. So mathematicians got really angry and wanted there to always be zeroes with polynomials of degree at least one (wanted an "algebraically closed" field), and created some arbitrary number j such that j = sqrt(-1). All the rules sort of fall into place from there (though they are more accurately reorganized differently-- specifically, you formally can't actually say "hey this number is the square root of negative one"). If there's that number j, you can get multiples of j. And you can add real numbers to j, so then you've got complex numbers. The operations with complex numbers are similar to operations with binomials (deliberately so).

The real problem with complexes isn't in all this, but in the fact that you can't define a system whereby you can get the ordinary rules for less-than and greater-than. So really, you get to where you don't define it at all. It doesn't make sense in a two-dimensional space. So in all honesty, I can't actually answer "give me an exaple of a number squared that is <= 0", though "j" makes sense if you treat its square as a real number instead of a complex number.

As for uses, well, I personally used them most when working with fractals. The idea behind the mandelbrot fractal is that it's a way of graphing z = z^2 + c and its divergence along the real-imaginary axes.

Answer 3

You might also ask why do negative numbers exist? They exist because you want to represent solutions to certain equations like: x + 5 = 0. The same thing applies for imaginary numbers, you want to compactly represent solutions to equations of the form: x^2 + 1 = 0.

Here's one way I've seen them being used in practice. In EE you are often dealing with functions that are sine waves, or that can be decomposed into sine waves. (See for example Fourier Series).

Therefore, you will often see solutions to equations of the form:

f(t) = A*cos(wt)

Furthermore, often you want to represent functions that are shifted by some phase from this function. A 90 degree phase shift will give you a sin function.

g(t) = B*sin(wt)

You can get any arbitrary phase shift by combining these two functions (called inphase and quadrature components).

h(t) = Acos(wt) + iB*sin(wt)

The key here is that in a linear system: if f(t) and g(t) solve an equation, h(t) will also solve the same equation. So, now we have a generic solution to the equation h(t).

The nice thing about h(t) is that it can be written compactly as

h(t) = Cexp(wt+theta)

Using the fact that exp(iw) = cos(w)+i*sin(w).

There is really nothing extraordinarily deep about any of this. It is merely exploiting a mathematical identity to compactly represent a common solution to a wide variety of equations.

Answer 4

If the question is "Do imaginary numbers exist?" or "How do imaginary numbers exist?" then it is not a question for a programmer. It might not even be a question for a mathematician, but rather a metaphysician or philosopher of mathematics, although a mathematician may feel the need to justify their existence in the field. It's useful to begin with a discussion of how numbers exist at all (quite a few mathematicians who have approached this question are Platonists, fyi). Some insist that imaginary numbers (as the early Whitehead did) are a practical convenience. But then, if imaginary numbers are merely a practical convenience, what does that say about mathematics? You can't just explain away imaginary numbers as a mere practical tool or a pair of real numbers without having to account for both pairs and the general consequences of them being "practical". Others insist in the existence of imaginary numbers, arguing that their non-existence would undermine physical theories that make heavy use of them (QM is knee-deep in complex Hilbert spaces). The problem is beyond the scope of this website, I believe.

If your question is much more down to earth e.g. how does one express imaginary numbers in software, then the answer above (a pair of reals, along with defined operations of them) is it.

Answer 5

Well, for the programmer:

class complex {
public:
  double real;
  double imaginary;

  complex(double a_real) : real(a_real), imaginary(0.0) { }
  complex(double a_real, double a_imaginary) : real(a_real), imaginary(a_imaginary) { }

  complex operator+(const complex &other) {
    return complex(
        real + other.real,
        imaginary + other.imaginary);
  }
  complex operator*(const complex &other) {
    return complex(
        real*other.real - imaginary*other.imaginary,
        real*other.imaginary + imaginary*other.real);
  }

  bool operator==(const complex &other) {
    return (real == other.real) && (imaginary == other.imaginary);
  }
};

That's basically all there is. Complex numbers are just pairs of real numbers, for which special overloads of +, * and == get defined. And these operations really just get defined like this. Then it turns out that these pairs of numbers with these operations fit in nicely with the rest of mathematics, so they get a special name.

They are not so much numbers like in "counting", but more like in "can be manipulated with +, -, *, ... and don't cause problems when mixed with 'conventional' numbers". They are important because they fill the holes left by real numbers, like that there's no number that has a square of -1. Now you have complex(0, 1) * complex(0, 1) == -1.0 which is a helpful notation, since you don't have to treat negative numbers specially anymore in these cases. (And, as it turns out, basically all other special cases are not needed anymore, when you use complex numbers)

Answer 6

I don't want to turn this site into math overflow, but for those who are interested: Check out "An Imaginary Tale: The Story of sqrt(-1)" by Paul J. Nahin. It talks about all the history and various applications of imaginary numbers in a fun and exciting way. That book is what made me decide to pursue a degree in mathematics when I read it 7 years ago (and I was thinking art). Great read!!

Answer 7

In electrical engineering, the impedance Z of an inductor is jwL, where w = 2*pi*f (frequency) and j (sqrt(-1))means it leads by 90 degrees, while for a capacitor Z = 1/jwc = -j/wc which is -90deg/wc so that it lags a simple resistor by 90 deg.

Answer 8

The main point is that you add numbers which you define to be solutions to quadratic equations like x²= -1. Name one solution to that equation i, the computation rules for i then follow from that equation.

This is similar to defining negative numbers as the solution of equations like 2 + x = 1 when you only knew positive numbers, or fractions as solutions to equations like 2x = 1 when you only knew integers.

Answer 9

It might be easiest to stop trying to understand how a number can be a square root of a negative number, and just carry on with the assumption that it is.

So (using the i as the square root of -1):

(3+5i)*(2-i)
= (3+5i)*2 + (3+5i)*(-i)
= 6 + 10i -3i - 5i * i
= 6 + (10 -3)*i - 5 * (-1)
= 6 + 7i + 5
= 11 + 7i

works according to the standard rules of maths (remembering that i squared equals -1 on line four).

Answer 10

An imaginary number is a real number multiplied by the imaginary unit i. i is defined as:

i == sqrt(-1)

So:

i * i == -1

Using this definition you can obtain the square root of a negative number like this:

   sqrt(-3)
== sqrt(3 * -1)
== sqrt(3 * i * i) // Replace '-1' with 'i squared'
== sqrt(3) * i     // Square root of 'i squared' is 'i' so move it out of sqrt()

And your final answer is the real number sqrt(3) multiplied by the imaginary unit i.

Answer 11

A short answer: Real numbers are one-dimensional, imaginary numbers add a second dimension to the equation and some weird stuff happens if you multiply...

Answer 12

If you're interested in finding a simple application and if you're familiar with matrices, it's sometimes useful to use complex numbers to transform a perfectly real matrice into a triangular one in the complex space, and it makes computation on it a bit easier.

The result is of course perfectly real.

Answer 13

Great answers so far (really like Devin's!)

One more point:

One of the first uses of complex numbers (although they were not called that way at the time) was as an intermediate step in solving equations of the 3rd degree. link

Again, this is purely an instrument that is used to answer real problems with real numbers having physical meaning.